
分析 根据万有引力提供向心力,每个星体的质量都是M,两者相距L,所以每一个的轨道半径都是$\frac{1}{2}$L,由$\frac{GMM}{{L}^{2}}=\frac{M•4{π}^{2}r}{{T}^{2}}$即可求出双星系统的运动周期.
解答 解:根据万有引力提供向心力得,$\frac{GMM}{{L}^{2}}=M(\frac{2π}{{T}_{计算}})^{2}•\frac{L}{2}$,
解得${T}_{计算}=2π\sqrt{\frac{{L}^{3}}{2GM}}$.
答:该双星系统的运动周期是$2π\sqrt{\frac{{L}^{3}}{2GM}}$.
点评 本题关键找出向心力来源,然后根据牛顿第二定律列方程求解,要细心,不难.


科目:高中物理 来源: 题型:多选题
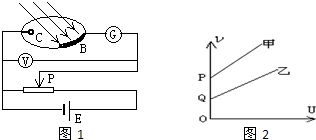
| A. | 金属甲的逸出功大于乙的 | |
| B. | 甲、乙两条直线一定是平行的(图中画的是不平行的) | |
| C. | 金属甲的逸出功小于乙的 | |
| D. | 甲、乙两条直线一定是不平行的 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
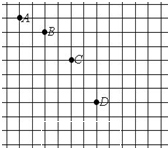 如图,在“研究平抛物体的运动”的实验中,用一张印有小格子的纸记录轨迹,小方格的边长L=1.25cm,若小球在运动途中的几个位置如图中的A、B、C、D所示,则
如图,在“研究平抛物体的运动”的实验中,用一张印有小格子的纸记录轨迹,小方格的边长L=1.25cm,若小球在运动途中的几个位置如图中的A、B、C、D所示,则查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 合运动与分运动体现了等效替代的思想 | |
| B. | 合运动与分运动具有等时性的特点 | |
| C. | 分运动都是匀速直线运动,它们的合运动可能是匀变速直线运动 | |
| D. | 同一物体的各分运动可能相互影响 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
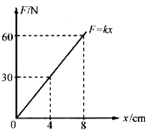 一根弹簧的弹力-位移图线如图所示,那么弹簧由伸长量8cm变到伸长量4cm的过程中,弹力所做的功和弹性势能的变化量为( )
一根弹簧的弹力-位移图线如图所示,那么弹簧由伸长量8cm变到伸长量4cm的过程中,弹力所做的功和弹性势能的变化量为( )| A. | 3.6J,-3.6J | B. | -3.6J,3.6J | C. | 1.8J,-1.8J | D. | -1.8J,1.8J |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
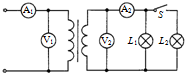 如图所示,理想变压器原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,交流电压表V1、V2和电流表A1、A2均为理想电表,导线电阻不计.当开关S闭合后( )
如图所示,理想变压器原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,交流电压表V1、V2和电流表A1、A2均为理想电表,导线电阻不计.当开关S闭合后( )| A. | A1示数变大,A1与A2示数的比值变大 | |
| B. | A1示数变大,A1与A2示数的比值不变 | |
| C. | V2示数变小,V1与V2示数的比值变大 | |
| D. | V2示数不变,V1与V2示数的比值不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
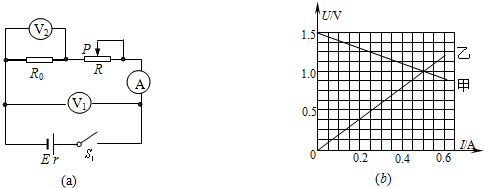
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com