
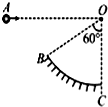
 如图所示,BC是半径为R的竖直面内的圆弧轨道,轨道末端C在圆心O的正下方,∠BOC=60°,将质量为m的小球,从与O等高的A点水平抛出,小球恰好从B点沿圆弧切线方向进入圆轨道,由于小球与圆弧之间有摩擦,能够使小球从B到C做匀速圆周运动.重力加速度大小为g.则( )
如图所示,BC是半径为R的竖直面内的圆弧轨道,轨道末端C在圆心O的正下方,∠BOC=60°,将质量为m的小球,从与O等高的A点水平抛出,小球恰好从B点沿圆弧切线方向进入圆轨道,由于小球与圆弧之间有摩擦,能够使小球从B到C做匀速圆周运动.重力加速度大小为g.则( )| A. | 从B到C,小球克服摩擦力做功为mgR | |
| B. | 从B到C,小球与轨道之间摩擦力逐渐减小 | |
| C. | 在C点,小球对轨道的压力大小等于mg | |
| D. | A、B两点间的距离为$\sqrt{\frac{7}{12}}$R |
分析 小球进入轨道前做平抛运动,应用平抛运动规律可以求出小球的初速度、小球的水平与竖直位移,从而求出A、B两点的距离,由牛顿第二定律与牛顿第三定律可以求出小球对轨道的压力.
解答 解:A、小球做从A到B做平抛运动,在B点,小球速度方向偏角θ=60°,
则$tan60°=\frac{{v}_{y}}{{v}_{A}}$,vy=gt
竖直方向的位移y=Rcos60°=$\frac{1}{2}g{t}^{2}$
水平方向的位移x=vAt
解得x=$\frac{\sqrt{3}}{3}R$
则A、B两点的距离${x}_{AB}=\sqrt{{x}^{2}+{y}^{2}}=\sqrt{\frac{7}{12}}R$,
在B点时小球的速度$v=\sqrt{{{v}_{A}}^{2}+{{v}_{y}}^{2}}=\frac{2\sqrt{3gR}}{3}$
球从B到C做匀速圆周运动,则由能量守恒定律可知
小球克服摩擦力做的功等于重力做的功${W}_{G}=mg(R-Rcos60°)=\frac{1}{2}mgR$,A错误,D正确;
B、从B到C,小球做匀速圆周运动,合外力指向圆心,则沿着速度方向的合力为零,即摩擦力等于重力沿速度方向的分力,而重力沿速度方向的分力逐渐减小,则摩擦力逐渐减小,由牛顿第三定律可知小球对轨道之间摩擦力逐渐减小,故B正确;
C、在C点,轨道对小球的支持力设为FN
则有${F}_{N}-mg=m\frac{{v}^{2}}{R}$
解得FN=$\frac{7}{3}mg$,由牛顿第三定律可知,在C点小球对轨道的压力也为$\frac{7}{3}mg$,故C错误;
故选:BD
点评 本题考查了平抛运动和圆周运动,分析清楚小球运动过程、应用运动的合成与分解、运动学公式、牛顿第二定律即可正确解题.


科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
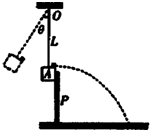 如图所示装置可用来验证机械能守恒定律.摆锤A栓在长L的轻绳一端,另一端固定在O点,在A上放一个小铁片,现将摆锤拉起,使绳偏离O竖直方向成θ角时由静止开始释放摆锤,当其到达最低位置时,受到竖直挡板P阻挡而停止运动,之后铁片将飞离摆锤而做平抛运动.
如图所示装置可用来验证机械能守恒定律.摆锤A栓在长L的轻绳一端,另一端固定在O点,在A上放一个小铁片,现将摆锤拉起,使绳偏离O竖直方向成θ角时由静止开始释放摆锤,当其到达最低位置时,受到竖直挡板P阻挡而停止运动,之后铁片将飞离摆锤而做平抛运动.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
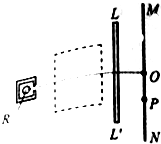 如图,R为真空室内一放射源,LL′为一张薄纸板,MN为荧光屏,放射源正对荧光屏的中心O点射出α、β、γ三种射线.若在虚线框内加上垂直于线框平面的匀强磁场时,荧光屏上只观察到O、P两个亮点,则打在O点的是γ射线,虚线框内磁场的方向向里(选填“向里”或“向外”).
如图,R为真空室内一放射源,LL′为一张薄纸板,MN为荧光屏,放射源正对荧光屏的中心O点射出α、β、γ三种射线.若在虚线框内加上垂直于线框平面的匀强磁场时,荧光屏上只观察到O、P两个亮点,则打在O点的是γ射线,虚线框内磁场的方向向里(选填“向里”或“向外”).查看答案和解析>>
科目:高中物理 来源: 题型:多选题
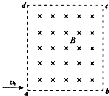 如图所示,边长为L的正方形区域abcd内存在着匀强磁场.一个质量为m、电荷量为q、初速度为v0的带电粒子从a点沿ab方向进入磁场,不计重力,则( )
如图所示,边长为L的正方形区域abcd内存在着匀强磁场.一个质量为m、电荷量为q、初速度为v0的带电粒子从a点沿ab方向进入磁场,不计重力,则( )| A. | 若粒子恰好从c点离开磁场,则磁感应强度B=$\frac{m{v}_{0}}{2qL}$ | |
| B. | 若粒子恰好从d离开磁场,则磁感应强度B=$\frac{2m{v}_{0}}{qL}$ | |
| C. | 若粒子恰好从bc边的中点离开磁场,则磁感应强度B=$\frac{4m{v}_{0}}{5qL}$ | |
| D. | 粒子从c点离开磁场时的动能大于从bc边的中点离开磁场时的动能 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 伽利略研究自由落体运动时,由于物体下落时间太短,不易测量,因此采用了“冲淡重力”的方法来测量时间,然后再把得出的结论合理外推 | |
| B. | 根据速度定义式,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了微元法方法 | |
| C. | 由a=$\frac{△v}{△t}$可知,物体的加速度又叫做速度的变化率,其值由比值$\frac{△v}{△t}$决定 | |
| D. | 在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了极限思想方法 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com