
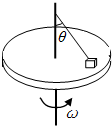
 ��ͼ��ʾ��ˮƽת̨����һ������Ϊm����飬�ó�ΪL��ϸ�������������ת���ϣ�ϸ������ֱת��ļн�Ϊ�Ƚǣ���ʱ��������Ϊ�㣬�����ת̨�䶯Ħ������Ϊ�̣��̣�tan�ȣ������Ħ�������ڻ���Ħ�����������ת̨�ɾ�ֹ��ʼ��������ת����������˵������ȷ���ǣ�������
��ͼ��ʾ��ˮƽת̨����һ������Ϊm����飬�ó�ΪL��ϸ�������������ת���ϣ�ϸ������ֱת��ļн�Ϊ�Ƚǣ���ʱ��������Ϊ�㣬�����ת̨�䶯Ħ������Ϊ�̣��̣�tan�ȣ������Ħ�������ڻ���Ħ�����������ת̨�ɾ�ֹ��ʼ��������ת����������˵������ȷ���ǣ�������| A�� | ��ת̨�Ħ�=$\sqrt{\frac{��g}{2Lsin��}}$ʱ������ܵ��ĸ������� | |
| B�� | ��ת̨�Ħ�=$\sqrt{\frac{��g}{Lsin��}}$ʱ��ϸ��ǡ�ò������� | |
| C�� | ��ת̨�Ħ�=$\sqrt{\frac{2g}{3Lcos��}}$ʱ�����ǡ�ö�ת̨��ѹ�� | |
| D�� | ��ת̨�Ħ�=$\sqrt{\frac{g}{Lcos��}}$ʱ��ת̨��������Ĺ�Ϊ$\frac{mgLsi{n}^{2}��}{2cos��}$ |
���� ��������������֪����뿪Բ��ǰ����F=f+Tsin��=$m\frac{{v}^{2}}{r}$��N+Tcos��=mg�����ݶ��ܶ���֪W=Ek=$\frac{1}{2}m{v}^{2}$
Ȼ������ٽ������������������ܱ仯��
��� �⣺A����ת̨�Ľ��ٶȱȽ�Сʱ�����ֻ��������֧������Ħ��������ϸ��ǡ��Ҫ��������ʱ��
$��mg=m{��}_{1}^{2}��Lsin�ȣ�$��
��ã�${��}_{1}=\sqrt{\frac{��g}{Lsin��}}$������$\sqrt{\frac{��g}{2Lsin��}}$��${��}_{1}=\sqrt{\frac{��g}{Lsin��}}$�����Ե���=${��}_{1}=\sqrt{\frac{��g}{Lsin��}}$ʱ��ϸ��������Ϊ�㣬��$��=\sqrt{\frac{��g}{2Lsin��}}$�����ֻ�ܵ�������֧������Ħ���������ã���A����B��ȷ��C����
D�����ٶȵ�����ϸ���ϵ������������ǡ��Ҫ�뿪ת̨ʱ������ܵ�������ϸ�������������ã���
$mgtan��=m{��}_{2}^{2}��Lsin�ȣ�$
��ã�${��}_{2}=\sqrt{\frac{g}{Lcos��}}$��
����=$\sqrt{\frac{g}{Lcos��}}$ʱ��С��ǡ��Ҫ�뿪ת̨��ת̨��������Ĺ�ת��Ϊ���Ķ��ܣ����ԣ�W=$\frac{1}{2}m{v}^{2}=\frac{1}{2}m��{��}_{2}•Lsin�ȣ�^{2}$=$\frac{mgLsi{n}^{2}��}{2cos��}$����D��ȷ��
��ѡ��BD
���� ���⿼��ţ���˶����ɺ��ܹ�ϵ��Բ���˶��е�Ӧ�ã�ע���ٽ������ķ����������г�������ʱ��Ħ����Ϊ���Ħ������ת̨�����֧����Ϊ��ʱ��N=0��f=0����Ŀ���ѣ�����Ҳ�Ƚ��鷳��


 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
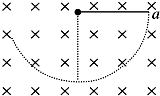 ��ͼ��ʾ���þ�Ե��������һ���������С������ǿ�ų��У��ְ�С�����������Ҳ�a�㣬������ˮƽ��ֱ����ֹ�ͷź�С������ֱƽ�������ذڶ�����С���˶������У������ж���ȷ���ǣ�������
��ͼ��ʾ���þ�Ե��������һ���������С������ǿ�ų��У��ְ�С�����������Ҳ�a�㣬������ˮƽ��ֱ����ֹ�ͷź�С������ֱƽ�������ذڶ�����С���˶������У������ж���ȷ���ǣ�������| A�� | С��ڵ�����������ߵ��a��Ҫ�� | |
| B�� | С��ÿ�ξ�����͵�ʱ��������������С��� | |
| C�� | С��ÿ�ξ�����͵�ʱ������������������ͬ | |
| D�� | С��ÿ�ξ�����͵�ʱ��������������С��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
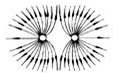
| A�� | �������ֵ�� | B�� | ����ͬ�ֵ�� | C�� | ��������� | D�� | ��������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ̫���ܵ���ǰѵ���ת��Ϊ���ܵ�װ�� | |
| B�� | ���ݵĶ����Ϊ0.05P | |
| C�� | ����������ĵĹ���Ϊ0.1P | |
| D�� | ��С���ݲ���һ����ͬ�ĵ��ݣ������ݶ������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
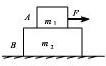 ��ͼ�������ֱ�Ϊm1��m2��A��B��ľ����ӷ��ڹ⻬��ˮƽ���ϣ�����ˮƽ����F������A�ϣ�A��B������Ծ�ֹ����A��B֮���Ħ����������F������B�ϣ�A��B������Ծ�ֹ��A��B֮���Ħ������������
��ͼ�������ֱ�Ϊm1��m2��A��B��ľ����ӷ��ڹ⻬��ˮƽ���ϣ�����ˮƽ����F������A�ϣ�A��B������Ծ�ֹ����A��B֮���Ħ����������F������B�ϣ�A��B������Ծ�ֹ��A��B֮���Ħ�������������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
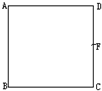 ��ͼ��ʾ��������ABCD������ǿ�糡�У����Ц�A=��B=0����D=U��F��ΪCD���е㣮����������B��Ϊ����ֽ����˳ʱ��ת����ABF�����ʱF��ĵ���Ϊ$\frac{{2\sqrt{5}}}{5}U$��
��ͼ��ʾ��������ABCD������ǿ�糡�У����Ц�A=��B=0����D=U��F��ΪCD���е㣮����������B��Ϊ����ֽ����˳ʱ��ת����ABF�����ʱF��ĵ���Ϊ$\frac{{2\sqrt{5}}}{5}U$���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 a��b������ƽֱ��·����ͬ������ʻ����v-tͼ����ͼ��ʾ����t=0ʱ��b����a��ǰ������Ϊx0������t1ʱ���ڣ�a����λ��Ϊx��������˵������ȷ���ǣ�������
a��b������ƽֱ��·����ͬ������ʻ����v-tͼ����ͼ��ʾ����t=0ʱ��b����a��ǰ������Ϊx0������t1ʱ���ڣ�a����λ��Ϊx��������˵������ȷ���ǣ�������| A�� | ��a��b��t1ʱ����������x0=$\frac{2}{3}$x | |
| B�� | ��a��b��$\frac{{t}_{1}}{2}$ʱ�����������´�����ʱ��Ϊ2t1 | |
| C�� | ��a��b��$\frac{{t}_{1}}{2}$ʱ����������x0=$\frac{x}{2}$ | |
| D�� | ��a��b��t1ʱ�����������´�����ʱ��Ϊ2t1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
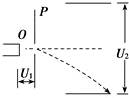 ��ͼ��ʾ����ֹ�ĵ����ڼ��ٵ�ѹU1�������¼����˶����ִ�ֱ����ƽ�н������ĵ糡����ƫת��ѹU2��������ƫתһ�ξ��룮���ܳ�ƫת�糡�£�ƫת�Ƕ�һ��������ǣ�������
��ͼ��ʾ����ֹ�ĵ����ڼ��ٵ�ѹU1�������¼����˶����ִ�ֱ����ƽ�н������ĵ糡����ƫת��ѹU2��������ƫתһ�ξ��룮���ܳ�ƫת�糡�£�ƫת�Ƕ�һ��������ǣ�������| A�� | U1���� U2���� | B�� | U1��СU2���� | ||
| C�� | U1 ���� U2��С | D�� | U1��СU2��С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �����������ֹ��������������� | |
| B�� | �κξ�Ե������������ֹ������������� | |
| C�� | �����������ֹ���ɼ������� | |
| D�� | �����������ֹ������Ĵ�СԶС������֮��ľ��룬���Ӧ�ÿ��ض��� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com