
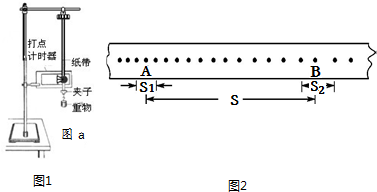
���� ��1�����ʵ����������Ҫ���ո�ʵ��ԭ�����˽�ʵ���������������������ݴ����Լ�ע�����
��2��ѡȡ���С�������������Ӷ���С������Ӱ�죻
��3��Ӧ�Ƚ�ͨ��Դ���ͷ�ֽ��������ƽ���ٶȵ���˲ʱ�ٶȣ��������������ܵı���ʽ��������⣻
��4�����ݼ�С���������ܵ������ӵĶ��ܣ�������⣮
��� �⣺��1������ʵ��ԭ������ʵ��װ�ã�����Ҫ�����ǿ̶ȳ߲������࣬
���ʽ����ʱ����Ҫ����220V������Ŵ���ʱ��ʹ�õĽ���6V��Դ����BD��ȷ��ACDEFG����
��2��Ϊ�˼�Сʵ���������ҵ�����Ӧѡȡ���С��������
���ѡȡ300g��С����B��ȷ��ACD����
��3��Ϊ����ֽ���Ͼ�����Ĵ�㣬���ֽ���������ʣ����Ҫ�ȴ����ͷ�ֽ����
����ƽ���ٶȵ���˲ʱ�ٶȣ���ô����A��ʱ��ֽ�����ٶ�ΪvA=$\frac{{S}_{1}}{2T}$��
��A��B�Ĺ�����������������ܵļ�С��Ϊ��EP=mgS��
��4��Ϊ����֤��������������л�е���غ㣬��ֻ����֤�Ƿ������С����������Լ�������ӵĶ��ܣ�mgs=$\frac{1}{2}m��{v}_{B}^{2}-{v}_{A}^{2}��$
����gs��$\frac{{s}_{2}^{2}-{s}_{1}^{2}}{8{T}^{2}}$��
�ʴ�Ϊ����1��BD��
��2��B��
��3����ͨ��Դ���ͷ����$\frac{{S}_{1}}{2T}$��mgS����4��C��
���� ���������Ŵ���ʱ���������������˲ʱ�ٶȵķ���������Ӵ���Դ���ͷ�ֽ�����Ⱥ��ϵ��ע���ܷ���֤��������������л�е���غ㣬Ҫ���Ƿ��ܵ�����Ӱ�죮


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���ļ��ٶ� | B�� | ���� | C�� | ���ٶ� | D�� | λ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 һ������Ϊm��С�����ذ뾶ΪR�Ĺ̶���Բ����ϱ�Ե�ɾ�ֹ���£�����Բ�ײ����ʣ�
һ������Ϊm��С�����ذ뾶ΪR�Ĺ̶���Բ����ϱ�Ե�ɾ�ֹ���£�����Բ�ײ����ʣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{7}$m/s | B�� | 1 m/s | C�� | $\sqrt{5}$m/s | D�� | 5m/s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����ĺ�ɢ������ת���ĽǶȷ�ӳ����Ȼ���к�۹��̵ķ����� | |
| B�� | ţ�ٷ����������������ɣ�����һ����ʵ������������������ | |
| C�� | ��������ѧ�ҵڹ��ܽ���������˶���������� | |
| D�� | 20���ͳ�����������ѧ��ţ�ٽ�������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
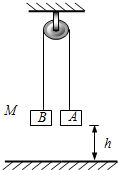 ��ͼ��ʾ��һ��ϸ���ƹ��⻬�Ķ����֣����˷ֱ�ϵסA��B�����壬������M��Ϊ2kg��ʹA��B��ֹ��ͬһ�߶ȣ���ظ߶�hΪ1m��������ķ�һ����Ϊ1kg��С����C��A����ճ�����������ٶ�gȡ10m/s2�������㹻�������뻬�ֵ��������ƣ�A��B��C������Ϊ�ʵ㣮
��ͼ��ʾ��һ��ϸ���ƹ��⻬�Ķ����֣����˷ֱ�ϵסA��B�����壬������M��Ϊ2kg��ʹA��B��ֹ��ͬһ�߶ȣ���ظ߶�hΪ1m��������ķ�һ����Ϊ1kg��С����C��A����ճ�����������ٶ�gȡ10m/s2�������㹻�������뻬�ֵ��������ƣ�A��B��C������Ϊ�ʵ㣮�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ݹ�ʽv=$\sqrt{\frac{GM}{r}}$����֪�����˶������ٶȽ���С��$\frac{v}{\sqrt{2}}$ | |
| B�� | ���ݹ�ʽF=m$\frac{{v}^{2}}{r}$����֪�������������������С��ԭ����$\frac{1}{2}$ | |
| C�� | ���ݹ�ʽ��=$\frac{v}{r}$����֪���ǵĽ��ٶȽ���С��$\frac{��}{2}$ | |
| D�� | ����F=G$\frac{Mm}{{r}^{2}}$����֪���ǵ���������СΪԭ����$\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
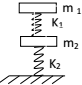 ��ͼ��ʾ����ľ��������ֱ�Ϊm1��m2�������ʵ��ɵľ���ϵ���ֱ�Ϊk1��k2������ľ��ѹ������ĵ����ϣ�����˩�ӣ�������ϵͳ����ƽ��״̬���ֻ��������������ľ�飬ֱ�������뿪���浯�ɣ��������������ľ���ƶ��ľ���Ϊ��������
��ͼ��ʾ����ľ��������ֱ�Ϊm1��m2�������ʵ��ɵľ���ϵ���ֱ�Ϊk1��k2������ľ��ѹ������ĵ����ϣ�����˩�ӣ�������ϵͳ����ƽ��״̬���ֻ��������������ľ�飬ֱ�������뿪���浯�ɣ��������������ľ���ƶ��ľ���Ϊ��������| A�� | $\frac{{m}_{1}g}{{k}_{1}}$ | B�� | $\frac{{m}_{1}g}{{k}_{1}}$+$\frac{{m}_{2}g}{{k}_{2}}$ | C�� | $\frac{{m}_{1}g}{{k}_{1}}$+$\frac{{m}_{1}g}{{k}_{2}}$ | D�� | $\frac{{��m}_{1}{+m}_{2}��g}{{k}_{1}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com