
| A. | 卫星运动的加速度为$\frac{4π^2(R+h)}{T^2}$ | |
| B. | 地球第一宇宙速度为$\frac{π(R+h)}{T}•\sqrt{\frac{R+h}{R}}$ | |
| C. | 地球表面的重力加速度为$\frac{4π^2(R+h)}{RT^2}$ | |
| D. | 地球的平均密度$\frac{3π(R+h)^3}{GT^2R^2}$ |
分析 根据圆周运动加速度表达式;
由引力提供向心力,即可求得地球的质量,与重力加速度,及平均密度;
同时由引力提供向心力,可求得第一宇宙速度.
解答 解:A、因卫星运动的加速度a=ω2r=$(\frac{2π}{T})^{2}(R+h)$=$\frac{4π^2(R+h)}{T^2}$,故A正确;
BD、因将天宫一号的运行轨道看做圆轨道,万有引力充当向心力,即$\frac{GMm}{(R+h)^{2}}=m\frac{4{π}^{2}}{{T}^{2}}(R+h)$,解得:M=$\frac{4{π}^{2}(R+h)^{3}}{G{T}^{2}}$,
那么地球的平均密度ρ=$\frac{M}{\frac{4π{R}^{3}}{3}}$=$\frac{3π(R+h)^3}{GT^2R^2}$,而地球的第一宇宙速度为v=$\sqrt{\frac{GM}{R}}$=$\frac{2π(R+h)}{T}$$•\sqrt{\frac{R+h}{R}}$,故B错误,D正确;
C、地球表面的重力加速度g=$\frac{GM}{{R}^{2}}$=$\frac{4{π}^{2}(R+h)^{3}}{{R}^{2}{T}^{2}}$,故C错误;
故选:AD.
点评 考查牛顿第二定律的应用,掌握万有引力定律与向心力表达式,理解平均密度是质量除以自身体积,不是轨道半径对应的体积.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 甲在运行时的速度小于第一宇宙速度 | |
| B. | 乙在运行时的速度大于第一宇宙速度 | |
| C. | 甲在运行时能经过北极的正上方 | |
| D. | 甲在运行时只能在赤道的正上方 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 若该波沿x轴向右传播,则图乙可表示质点Q的振动图象 | |
| B. | 若该波沿x轴向右传播,则图乙可表示质点P的振动图象 | |
| C. | 若图乙表示质点Q的振动图象,则波速一定为5m/s | |
| D. | 不论该波沿x轴向右传播,还是沿x轴向左传播,P、Q两质点的振动方形相反 | |
| E. | 再经$\frac{1}{4}$个周期,质点P一定到达波峰位置 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 转动时U-I特性曲线,如图甲所示,该同学利用图乙的实验电路研究电动机的转动情况,电路中使用恒压电源(输出电压值固定),R1是定值电阻(阻值为10Ω),R2是滑动变阻器,
转动时U-I特性曲线,如图甲所示,该同学利用图乙的实验电路研究电动机的转动情况,电路中使用恒压电源(输出电压值固定),R1是定值电阻(阻值为10Ω),R2是滑动变阻器, 是理想电流表,实验操作步骤如下:
是理想电流表,实验操作步骤如下: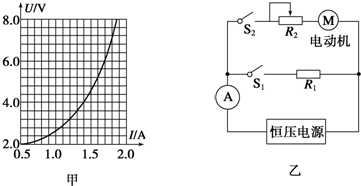
 实际消耗的电功率为5.6W,滑动变阻器接入电路中的阻值为1.43Ω.
实际消耗的电功率为5.6W,滑动变阻器接入电路中的阻值为1.43Ω.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 右端带有$\frac{1}{4}$光滑圆弧轨道质量为M的小车静置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上小车,关于小球此后的运动情况,以下说法正确的是( )
右端带有$\frac{1}{4}$光滑圆弧轨道质量为M的小车静置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上小车,关于小球此后的运动情况,以下说法正确的是( )| A. | 小球速度为零时,上升到圆弧轨道的最高点 | |
| B. | 小球可能离开小车水平向左做平抛运动 | |
| C. | 小球可能离开小车做自由落体运动 | |
| D. | 小球可能离开小车水平向右做平抛运动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com