
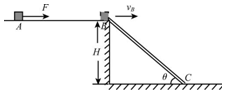
 一水平轨道AB距离地面的高度为H=0.8m,A、B点间的距离为2.5m,一长度合适的薄木板两端分别搁在轨道末端点和水平地面之间,构成倾角为θ=45°的斜面,如图所示.一质量为m=1kg的小物体,在水平轨道上运动,小物体与轨道AB间的动摩擦因数μ=0.2,设小物体从B点水平抛出时的速度为vB.(不计空气阻力,不考虑物体碰撞木板或地面后的运动,取g=10m/s2)
一水平轨道AB距离地面的高度为H=0.8m,A、B点间的距离为2.5m,一长度合适的薄木板两端分别搁在轨道末端点和水平地面之间,构成倾角为θ=45°的斜面,如图所示.一质量为m=1kg的小物体,在水平轨道上运动,小物体与轨道AB间的动摩擦因数μ=0.2,设小物体从B点水平抛出时的速度为vB.(不计空气阻力,不考虑物体碰撞木板或地面后的运动,取g=10m/s2)分析 (1)根据平抛运动的规律求解下落时间,再根据水平方向的匀速直线运动求解速度;
(2)若vB=1m/s,落在斜面上时水平位移与竖直位移相等,根据位移关系求解竖直方向的速度,再根据位移速度关系求解竖直方向的位移,进而求出s0;
(3)为使小物体能落到薄木板上,物体达到B点的速度范围为0<v<2m/s,根据动能定理求解力F的作用距离,再根据牛顿运动定律求解时间.
解答 解:(1)设物体做平抛运动的时间为t1,则:H=$\frac{1}{2}g{t}_{1}^{2}$,
解得:${t}_{1}=\sqrt{\frac{2H}{g}}=\sqrt{\frac{2×0.8}{10}}s=0.4s$,
水平位移x=H=0.8m,
根据平抛运动规律可得:${v}_{B}=\frac{x}{{t}_{1}}=\frac{0.8}{0.4}m/s=2m/s$,
所以物体的最小速度为2m/s;
(2)若vB=1m/s,落在斜面上时水平位移与竖直位移相等,则:
$\frac{{v}_{y}}{2}{t}_{2}={v}_{B}{t}_{2}$,
解得:vy=2vB=2m/s,
竖直方向的位移为h,则:$h=\frac{{v}_{y}^{2}}{2g}=\frac{4}{20}m=0.2m$,
则:${s}_{0}=\sqrt{2}h=0.2\sqrt{2}m$;
(3)当物体恰好到达B点时速度为零,力F的作用时间为tmin,作用距离为x1,
根据动能定理可得:$F{x}_{1}-μmg{L}_{AB}=0-\frac{1}{2}m{v}_{A}^{2}$,
解得:x1=1.5m;
有力F作用时的加速度为:a=$\frac{F-μmg}{m}=\frac{3-2}{1}m/{s}^{2}=1m/{s}^{2}$,
根据位移时间关系可得:${x}_{1}={v}_{A}{t}_{min}+\frac{1}{2}a{t}_{min}^{2}$,
解得:tmin=1s;
当物体到达B点时速度为v=2m/s,力F的作用时间最长为tmax,作用距离为x2,
根据动能定理可得:$F{x}_{2}-μmg{L}_{AB}=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{A}^{2}$,
解得:${x}_{2}=\frac{13}{6}m$,
根据位移时间关系可得:${x}_{2}={v}_{A}{t}_{max}+\frac{1}{2}a{t}_{max}^{2}$,
解得:tmax=1.3s,
所以F作用在小物体上时间范围为1s<t<1.3s;
答:(1)为使小物体直接落在水平地面上,vB至少为2m/s;
(2)若vB=1m/s,求小物体落到斜面上时距离B点的距离为$0.2\sqrt{2}$m;
(3)为使小物体能落到薄木板上,F作用在小物体上时间范围为1s<t<1.3s.
点评 本题主要是考查了平抛运动的规律、动能定理和牛顿第二定律的综合应用,知道平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动;知道加速度是联系静力学和运动学的桥梁.


 53随堂测系列答案
53随堂测系列答案科目:高中物理 来源: 题型:填空题
 处于坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时,波刚传播到x=40m处,波形如图所示,在x=400m处有一接受器(图中未画出),则下列说法正确的是ACD(填正确答案标号)
处于坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时,波刚传播到x=40m处,波形如图所示,在x=400m处有一接受器(图中未画出),则下列说法正确的是ACD(填正确答案标号)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量m板=2.0kg的木板静置在光滑水平面上,木板上表面右端放一个质量m=0.8kg的物块,它们之间的动摩擦因数μ=0.15,质量m0=0.4kg的滑块以速度v0=6m/s沿水平面正碰木板的左端(碰撞时间极短),碰后连在一起沿水平地面运动,经过一段时间,物块相对木板向左滑动了一段距离d后与木板共同运动,求物块m相对木板滑动的距离d是多少.(取g=10m/s)
如图所示,质量m板=2.0kg的木板静置在光滑水平面上,木板上表面右端放一个质量m=0.8kg的物块,它们之间的动摩擦因数μ=0.15,质量m0=0.4kg的滑块以速度v0=6m/s沿水平面正碰木板的左端(碰撞时间极短),碰后连在一起沿水平地面运动,经过一段时间,物块相对木板向左滑动了一段距离d后与木板共同运动,求物块m相对木板滑动的距离d是多少.(取g=10m/s)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 物体都具有保持原来运动状态的属性,即惯性 | |
| B. | 力不是维持物体运动的原因 | |
| C. | 忽略空气阻力,重物与轻物下落得同样块 | |
| D. | 物体间的相互作用力总是大小相等、方向相反 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 支撑脚蹬地的瞬间,地面对脚的支持力大于脚对地面的压力 | |
| B. | 支撑脚蹬地的瞬间,地面受到向后的摩擦力 | |
| C. | 支撑脚离地后,他还受到向前冲的力,以至于能很快地通过栏架 | |
| D. | 跨栏落地后,脚对地面的压力小于地面的支持力 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
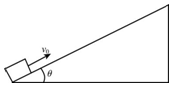 如图所示,有一倾角θ=37°的足够长的固定的斜面,一物体以平行于斜面的初速度v0=8m/s从斜面底端开始沿斜面向上滑行,已知物体与斜面间动摩擦因数为μ=0.25,(已知sin37°=0.6,cos37°=0.8,g取10m/s2.)
如图所示,有一倾角θ=37°的足够长的固定的斜面,一物体以平行于斜面的初速度v0=8m/s从斜面底端开始沿斜面向上滑行,已知物体与斜面间动摩擦因数为μ=0.25,(已知sin37°=0.6,cos37°=0.8,g取10m/s2.)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
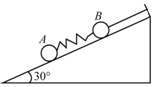 如图所示,质量相等的A、B两小球分别连在弹簧两端,B小球用细绳固定在倾角为30°的光滑斜面上,若不计算弹簧质量,在细绳被剪断的瞬间,关于A、B两小球的加速度大小,正确的是( )
如图所示,质量相等的A、B两小球分别连在弹簧两端,B小球用细绳固定在倾角为30°的光滑斜面上,若不计算弹簧质量,在细绳被剪断的瞬间,关于A、B两小球的加速度大小,正确的是( )| A. | aA=g | B. | aA=0.5g | C. | aB=g | D. | aB=0.5g |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
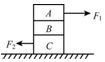 如图所示,A、B、C三个物体,叠放在水平地面上,A受5N的水平拉力F1,C受3N的水平拉力F2,这三个物体都保持静止,则( )
如图所示,A、B、C三个物体,叠放在水平地面上,A受5N的水平拉力F1,C受3N的水平拉力F2,这三个物体都保持静止,则( )| A. | B对C的静摩擦力大小为0N | |
| B. | A对B的静摩擦力大小为5N,方向水平向右 | |
| C. | C对B的静摩擦力大小为5N,方向水平向左 | |
| D. | 地面对C的静摩擦力大小为2N,方向水平向左 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com