
 ��ͼ��ʾ��AB����ֱ���ڵİ�Բ����ˮƽֱ������A����е����ΪQ1�ĵ��ɣ���B�������һ���ɣ�һ�����Ϊq�Ĵ��������Բ���ϵ�C��պô��ھ�ֹ״̬��A��C������ˮƽ����ļн�Ϊ�ȣ�Բ���İ뾶ΪR��������˵����ȷ���ǣ�������
��ͼ��ʾ��AB����ֱ���ڵİ�Բ����ˮƽֱ������A����е����ΪQ1�ĵ��ɣ���B�������һ���ɣ�һ�����Ϊq�Ĵ��������Բ���ϵ�C��պô��ھ�ֹ״̬��A��C������ˮƽ����ļн�Ϊ�ȣ�Բ���İ뾶ΪR��������˵����ȷ���ǣ�������| A�� | �������ɺʹ�����һ��������ͬ�ֵ�� | |
| B�� | A��B���ĵ�ɿ��������ֵ�� | |
| C�� | B���ɵĵ���ΪQ1tan�� | |
| D�� | �����������Ϊ$\frac{kq{Q}_{1}}{4g{R}^{2}sin��co{s}^{2}��}$ |
���� ��A���һ����Q1����B���һ����Q2ʱ����С������������С���ܵ����ǿ��������ֱ���������ƽ��ͼ�����������Ĺ�ϵ�ж�������ɵĵ��Թ�ϵ���ٸ��ݼ��ι�ϵ����������������Ĺ�ϵ���Ӷ��ҵ�������ı�ֵ��
��� �⣺A���������ĵ����ͬ�ֵ��ʱ������ͼ����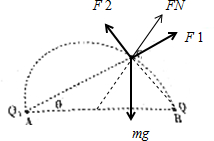
��ͼ��֪��F1��F2�ĺ�������������mg��С��ȣ������෴���п���F1��F2��FN�ĺ�����������С��ȣ������෴����������Դ���ƽ��״̬��
��Q1�ĵ����������������ĵ��Բ�ͬ����������ͼ��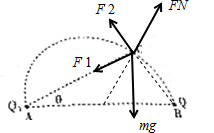
��ͼ��֪��F1��F2��FN�ĺ���������������С��ȣ������෴����������Դ���ƽ��״̬����A����B��ȷ��
C�����ڴ����������������δ֪��B����ɵĵ���δ֪�����Դ������֧�����ķ������С����δ֪�ģ����Բ��ܴ�A�ĵ���Q1�Լ�A��C������ˮƽ����ļн�Ϊ�����B�ĵ����Լ�������ĵ�������CD����
��ѡ��B
���� ����Ҫ�ܸ�����������С�������ƽ��ͼ��Ȼ����ݼ��ι�ϵ����������Ĵ�С��������С�Ĺ�ϵ��������ȷ�����������DZ���Ľ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һˮƽ���õ�ƽ�а����������������Ϊd��������ѹΪU0��A������磬B������磬�������Ϸ���һ������Ϊd�㹻������ǿ�ų����ų�����ֱֽ�����һ������Ϊm�������Ϊq�Ĵ���������������������A���Ե��ˮƽ������ٶ�v0���˵����������ڴ���ij������ʹ������ˮƽ�������ȼ����˶�������һ��ʱ������Ӵ�B��һ��С��N���˴ų������˴ų����ٶȷ�������ֱ���Ϸ���ļн�Ϊ37�㣮С��N����B���Ҷ˵ľ���ҲΪd��sin37��=0.6��������
��ͼ��ʾ��һˮƽ���õ�ƽ�а����������������Ϊd��������ѹΪU0��A������磬B������磬�������Ϸ���һ������Ϊd�㹻������ǿ�ų����ų�����ֱֽ�����һ������Ϊm�������Ϊq�Ĵ���������������������A���Ե��ˮƽ������ٶ�v0���˵����������ڴ���ij������ʹ������ˮƽ�������ȼ����˶�������һ��ʱ������Ӵ�B��һ��С��N���˴ų������˴ų����ٶȷ�������ֱ���Ϸ���ļн�Ϊ37�㣮С��N����B���Ҷ˵ľ���ҲΪd��sin37��=0.6���������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ������ˮ����ľ��ƿ�Ǻ���ʱľ�����Զ�����������������Ӽ�������õĽ�� | |
| B�� | ������ˮ����ľ��ƿ�Ǻ���ʱľ�����Զ������ǽ���ƿ�ڵĿ��������ߣ�ѹǿ����Ľ�� | |
| C�� | װ�IJ�̫���ı���ƿ�����ϳ�ʱ��ʱ����ʱľ��ƿ�Ǻ��ѱ���������������Ӽ��������õĽ�� | |
| D�� | װ�IJ�̫���ı���ƿ�����ϳ�ʱ��ʱ����ʱľ��ƿ�Ǻ��ѱ����DZ���ƿ�������¶ȵͣ�ѹǿ���ٵĽ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ˮƽ�̶�һ���㹻���Ĺ⻬ֱ�ˣ���������һ����Ϊm��С��A��A�����ֱ�����ɻ�����һ����Ϊl������ϸ��һ������A����һ����������Ϊ2m��С��B����ʼʱ������ֱ����ˮƽ�˳�30�㣮�ɾ�ֹ�ͷ�B�����°ڶ��Ĺ����У�����
ˮƽ�̶�һ���㹻���Ĺ⻬ֱ�ˣ���������һ����Ϊm��С��A��A�����ֱ�����ɻ�����һ����Ϊl������ϸ��һ������A����һ����������Ϊ2m��С��B����ʼʱ������ֱ����ˮƽ�˳�30�㣮�ɾ�ֹ�ͷ�B�����°ڶ��Ĺ����У������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ţ���ܽ�������������õĹ��� | |
| B�� | ����ʿ�����Ϊ�����������˶�״̬�ı��ԭ�����������˶���ԭ�� | |
| C�� | ��������õ����e����ֵ | |
| D�� | ��˹�ط��ֵ���ͨ��ʱ�����߸�����С���뷢��ƫת |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 һ���Ϊ��=37��Ĵֲ�б����һ�⻬�İ뾶R=0.9m����ֱԲ���������P�㣬O���ǹ��Բ�ģ�����ϵ�B������ߵ㣬D������͵㣬C�������ҵĵ㣬б���ϵ�A����B��ȸߣ�һ����m=1.0kg��С�����A������б�����µij��ٶ�v0�պ�����б���������˶���ͨ��P�㴦��С����Բ�����ǡ����������Բ���˶���g=10m/s2��sin37��=0.6��cos37��=0.8��������˵����ȷ���ǣ�������
һ���Ϊ��=37��Ĵֲ�б����һ�⻬�İ뾶R=0.9m����ֱԲ���������P�㣬O���ǹ��Բ�ģ�����ϵ�B������ߵ㣬D������͵㣬C�������ҵĵ㣬б���ϵ�A����B��ȸߣ�һ����m=1.0kg��С�����A������б�����µij��ٶ�v0�պ�����б���������˶���ͨ��P�㴦��С����Բ�����ǡ����������Բ���˶���g=10m/s2��sin37��=0.6��cos37��=0.8��������˵����ȷ���ǣ�������| A�� | v0=3m/s | |
| B�� | С�����б���Ķ�Ħ��������=0.6 | |
| C�� | С�����D��ʱ�Թ��ѹ��F0=60N | |
| D�� | С�����C���ܵ��ĺ�����ˮƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ٤�������о����������˶�ʱ����������ʵ�飮����һ��ͭ���������С���ɺ��Բ��ƣ���б�����ɾ�ֹ��ʼ���£������ظ������ϰٴ�ʵ�飮����ij��ʵ����٤�������������ģ���б������ȡ����λ��A��B��C����ͼ��ʾ����С��ֱ���A��B��Cλ�ôӾ�ֹ���£�A��B��C��б��˵ľ���ֱ�Ϊxl��x2��x3��С����A��B��C�˶���б��˵�ʱ��ֱ�Ϊt1��t2��t3���ٶȷֱ�Ϊvl��v2��v3�������й�ϵʽ����ȷ������٤��������֤��С���ع⻬б�������˶����ȱ���ֱ���˶����ǣ�������
٤�������о����������˶�ʱ����������ʵ�飮����һ��ͭ���������С���ɺ��Բ��ƣ���б�����ɾ�ֹ��ʼ���£������ظ������ϰٴ�ʵ�飮����ij��ʵ����٤�������������ģ���б������ȡ����λ��A��B��C����ͼ��ʾ����С��ֱ���A��B��Cλ�ôӾ�ֹ���£�A��B��C��б��˵ľ���ֱ�Ϊxl��x2��x3��С����A��B��C�˶���б��˵�ʱ��ֱ�Ϊt1��t2��t3���ٶȷֱ�Ϊvl��v2��v3�������й�ϵʽ����ȷ������٤��������֤��С���ع⻬б�������˶����ȱ���ֱ���˶����ǣ�������| A�� | $\frac{{v}_{1}}{{t}_{1}}$=$\frac{{v}_{2}}{{t}_{2}}$=$\frac{{v}_{3}}{{t}_{3}}$ | B�� | $\frac{{v}_{1}}{2}$=$\frac{{v}_{2}}{2}$=$\frac{{v}_{3}}{2}$ | ||
| C�� | $\frac{{x}_{1}}{{t}_{1}^{2}}$=$\frac{{x}_{2}}{{t}_{2}^{2}}$=$\frac{{x}_{3}}{{t}_{3}^{2}}$ | D�� | x1-x2=x2-x3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com