
 T,正离子运动的时间为t2=
T,正离子运动的时间为t2= T,而周期T=
T,而周期T=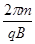 相同,则t1>t2.故A错误.
相同,则t1>t2.故A错误.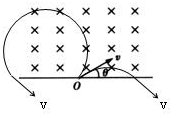
 ,由题意可知,正负离子质量、电荷量均相等,速度相同,B相同,则它们运动的轨道半径相同.故B正确.
,由题意可知,正负离子质量、电荷量均相等,速度相同,B相同,则它们运动的轨道半径相同.故B正确.

科目:高中物理 来源: 题型:
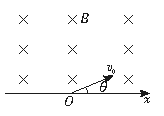
 如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹30°角.求正、负离子在磁场中运动半径比
如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹30°角.求正、负离子在磁场中运动半径比| r正 |
| r负 |
| t正 |
| t负 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中( )?
如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中( )?查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,x轴上方有竖直向下的匀强电场,从x轴A点(5
如图所示,x轴上方有竖直向下的匀强电场,从x轴A点(5| 3 |
| ||
| 2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中( )
如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中( )查看答案和解析>>
科目:高中物理 来源: 题型:
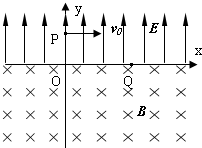 如图所示,x轴上方有一匀强电场,方向与y轴平行;x轴下方有一匀强磁场,方向垂直纸面向里.一质量为m、电量为-q(q>0)的粒子以速度v0从y轴上的P点平行x轴方向射入电场后,从x轴上的Q点进入磁场,并从坐标原点O离开磁场.已知OP=L,OQ=2L.不计重力和一切摩擦,求:
如图所示,x轴上方有一匀强电场,方向与y轴平行;x轴下方有一匀强磁场,方向垂直纸面向里.一质量为m、电量为-q(q>0)的粒子以速度v0从y轴上的P点平行x轴方向射入电场后,从x轴上的Q点进入磁场,并从坐标原点O离开磁场.已知OP=L,OQ=2L.不计重力和一切摩擦,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com