
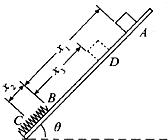
 为测定物块与木板间的动摩擦因数,小明同学设计了如图所示的实验装置.木板的倾角为θ,弹簧的一端固定在木板上,另一端位于木板上的B点.物块在木板上A点静止释放后沿木板滑下,压缩弹簧运动至C点后被弹回,上滑至D点时速度为零.测得AB间的距离为x1、BC间的距离为x2,BD间的距离为x3.实验中的弹簧可视为轻质弹簧.
为测定物块与木板间的动摩擦因数,小明同学设计了如图所示的实验装置.木板的倾角为θ,弹簧的一端固定在木板上,另一端位于木板上的B点.物块在木板上A点静止释放后沿木板滑下,压缩弹簧运动至C点后被弹回,上滑至D点时速度为零.测得AB间的距离为x1、BC间的距离为x2,BD间的距离为x3.实验中的弹簧可视为轻质弹簧.分析 (1)对ACD过程由动能定理进行分析,则可求得动摩擦因数;
(2)由功能关系可得出弹性势能的表达式;由题意可知达到最大速度时,合外力为零;再由动能定理可分析最大速度的表达式.
解答 解:(1)对ACD过程应用动能定理有:
mgsinθ(x1-x3)-μmg(x1+2x2+x3)=0
解得:μ=$\frac{({x}_{1}-{x}_{3})sinθ}{({x}_{1}+2{x}_{2}+{x}_{3})cosθ}$=$\frac{(0.4-0.25)×\frac{\sqrt{2}}{2}}{(0.4+0.1+0.25)×\frac{\sqrt{2}}{2}}$=0.2;
(2)①对AC过程,应用功能关系:
EP=(mgsinθ-μmgcosθ)(x1+x2)
②当物体的速度达最大时满足:
mgsinθ-μmgcosθ=kx
应用动能定理有:
(mgsinθ-μmgcosθ)(x1+x)-$\frac{1}{2}$kx2=$\frac{1}{2}$mvm2
解得最大速度为:vm=$\sqrt{2g(sinθ-μcosθ)({x}_{1}+\frac{(mgsinθ-μmgcosθ)}{k})-\frac{m{g}^{2}}{k}(sinθ-μcosθ)^{2}}$
答:(1)物块与木板间的动摩擦因数为0.2;
(2)最大速度为$\sqrt{2g(sinθ-μcosθ)({x}_{1}+\frac{(mgsinθ-μmgcosθ)}{k})-\frac{m{g}^{2}}{k}(sinθ-μcosθ)^{2}}$.
点评 本题考查了受力分析、判断物块动能如何变化、求动摩擦因数,分析清楚物体的运动过程、从能量角度分析问题、应用动能定理即可正确解题.


 考前必练系列答案
考前必练系列答案科目:高中物理 来源: 题型:选择题
| A. | $\frac{4{π}^{2}{r}^{2}(r-{r}_{1})}{G{T}^{2}}$ | B. | $\frac{4{π}^{2}{{r}_{1}}^{3}}{G{T}^{2}}$ | C. | $\frac{4{π}^{2}{r}^{2}}{G{T}^{2}}$ | D. | $\frac{4{π}^{2}{r}^{2}{r}_{1}}{G{T}^{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
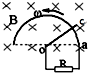 如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是( )
如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是( )| A. | $\frac{{B}^{2}{r}^{2}{ω}^{4}}{4R}$ | B. | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{4R}$ | C. | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{2R}$ | D. | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{9R}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
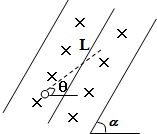 实线表示竖直平面内匀强电场的电场线,电场线与水平方面成α角,匀强磁场与电场正交,垂直纸面向里.有一带电液滴沿斜向上的虚线L做直线运动,L与水平方向成θ角,且α>θ,则下列说法中正确的是( )
实线表示竖直平面内匀强电场的电场线,电场线与水平方面成α角,匀强磁场与电场正交,垂直纸面向里.有一带电液滴沿斜向上的虚线L做直线运动,L与水平方向成θ角,且α>θ,则下列说法中正确的是( )| A. | 液滴一定做匀变速直线运动 | B. | 液滴一定带正电 | ||
| C. | 电场线的方向一定斜向上 | D. | 液滴有可能做匀速直线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
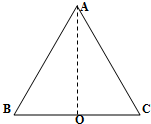 如图所示为一等边三角形的某种透明介质ABC,边长为L,折射率为$\frac{5}{3}$,底部中点O处有一点光源,试问能够从AB边射出光线的长度是多少?
如图所示为一等边三角形的某种透明介质ABC,边长为L,折射率为$\frac{5}{3}$,底部中点O处有一点光源,试问能够从AB边射出光线的长度是多少?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,是霍尔元件的原理示意图,如果用d表示薄片的厚度,k为霍尔系数,对于一个霍尔元件d、k为定值,如果保持电流I恒定,则可以验证UH随B的变化情况.下列说法错误的是( )
如图,是霍尔元件的原理示意图,如果用d表示薄片的厚度,k为霍尔系数,对于一个霍尔元件d、k为定值,如果保持电流I恒定,则可以验证UH随B的变化情况.下列说法错误的是( )| A. | 霍尔元件是一种磁传感器,即对磁场有敏感的反应 | |
| B. | 将永磁体的一个磁极逐渐靠近霍尔元件的工作面时,UH将变大 | |
| C. | 在测定地球赤道上的磁场强弱时,霍尔元件的工作面应保持水平 | |
| D. | 改变磁感线与霍尔元件工作面的夹角时UH将会发生变化 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 火星的密度为$\frac{2g}{3πGR}$ | |
| B. | 火星表面的重力加速度是$\frac{2g}{9}$ | |
| C. | 火星的第一宇宙速度与地球的第一宇宙速度之比为$\frac{2}{3}$ | |
| D. | 王跃在火星表面上能向上竖直跳起的最大高度也是h |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 两人的线速度相同,为0.4 m/s | |
| B. | 两人的角速度相同,为5.0 rad/s | |
| C. | 两人的运动半径相同,都是0.45 m | |
| D. | 两人的运动半径不同,甲的半径是0.3m、乙的半径是0.6 m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com