
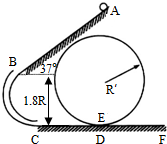
 如图所示,倾斜轨道AB的倾角为37°,CD、EF轨道水平,AB与CD通过光滑圆弧管道BC连接,CD右端与竖直光滑圆周轨道相连.小球可以从D进入该轨道,沿轨道内侧运动,从E滑出该轨道进入EF水平轨道.小球由静止从A点释放,已知AB长为5R,CD长为R,重力加速度为g,小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5,sin37°=0.6,cos37°=0.8,圆弧管道BC入口B与出口C的高度差为1.8R.求:(在运算中,根号中的数值无需算出)
如图所示,倾斜轨道AB的倾角为37°,CD、EF轨道水平,AB与CD通过光滑圆弧管道BC连接,CD右端与竖直光滑圆周轨道相连.小球可以从D进入该轨道,沿轨道内侧运动,从E滑出该轨道进入EF水平轨道.小球由静止从A点释放,已知AB长为5R,CD长为R,重力加速度为g,小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5,sin37°=0.6,cos37°=0.8,圆弧管道BC入口B与出口C的高度差为1.8R.求:(在运算中,根号中的数值无需算出)分析 (1)对球从A运动至C过程运用动能定理列式求解即可;
(2)在C点,重力和支持力的合力提供向心力;根据牛顿第二定律列式求解支持力;然后再结合牛顿第三定律求解压力;
(3)要使小球不脱离轨道,有两种情况:情况一:小球能滑过圆周轨道最高点,进入EF轨道.情况二:小球上滑至四分之一圆轨道的点(设为Q)时,速度减为零,然后滑回D.由动能定理列出等式求解.
解答 解:(1)设小球到达C点时速度为v,小球从A运动至C过程,由动能定理有:
mg(5Rsin37°+1.8R)-μmgcos37°•5R=$\frac{1}{2}m{v}_{C}^{2}$,
可得:vC=$\sqrt{\frac{28gR}{5}}$.
(2)小球沿BC轨道做圆周运动,设在C点时轨道对球的作用力为FN,由牛顿第二定律,有:
FN-mg=m$\frac{{v}_{C}^{2}}{r}$,
其中r满足:r+r•sin53°=1.8R,
联立上式可得:FN=6.6mg,
由牛顿第三定律可得,球对轨道的作用力为6.6mg,方向竖直向下.
(3)要使小球不脱离轨道,有两种情况:
情况一:小球能滑过圆周轨道最高点,进入EF轨道.则小球在最高点应满足:m$\frac{{v}_{P}^{2}}{R′}$≥mg
小球从C直到此最高点过程,由动能定理,有:
-μmgR-mg•2R′=$\frac{1}{2}$mvP2-$\frac{1}{2}$mvC2,
可得:R′≤$\frac{23}{25}$R=0.92R,
情况二:小球上滑至四分之一圆轨道的最高点时,速度减为零,然后滑回D.则由动能定理有:
-μmgR-mg•R′=0-$\frac{1}{2}$mvC2
解得:R′≥2.3R
所以要使小球不脱离轨道,竖直圆周轨道的半径R′应该满足R′≤0.92R或R′≥2.3R.
答:
(1)小球滑到斜面底端C时速度的大小是$\sqrt{\frac{28gR}{5}}$.
(2)小球刚到C时对轨道的作用力是6.6mg,方向竖直向下.
(3)要使小球在运动过程中不脱离轨道,竖直圆周轨道的半径R′应该满足R′≤0.92R或R′≥2.3R.
点评 此题要求熟练掌握动能定理、圆周运动等规律,包含知识点多,关键要知道小球在运动过程中不脱离轨道可能做完整的圆周运动,也可能只在四分之一圆轨道上运动.运用动能定理时,要明确所研究的过程,分析各个力所做的总功.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
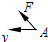 一物体以速度v运动,到达位置A开始受到向前但偏右的(观察者沿物体的运动方向看,下同)的合力,到达B时,合力改成与前进方向相同,到达C时,合力又突然改成向前但偏左,最终到达D.以下四图表示物体全程的运动轨迹,正确的是( )
一物体以速度v运动,到达位置A开始受到向前但偏右的(观察者沿物体的运动方向看,下同)的合力,到达B时,合力改成与前进方向相同,到达C时,合力又突然改成向前但偏左,最终到达D.以下四图表示物体全程的运动轨迹,正确的是( )| A. | 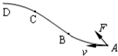 | B. |  | C. | 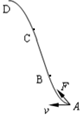 | D. | 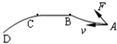 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
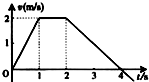
| A. | 0~1s内的平均速度是1m/s | |
| B. | 0~2s内的位移大小是3m | |
| C. | 0~1s内的加速度大小等于2~4s内的加速度大小 | |
| D. | 0~1s内的运动方向与2~4s内的运动方向相反 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 伽耳顿板可以演示统计规律.如图,让大量小球从上方漏斗形入口落下,最终小球都落在槽内.重复多次实验后发现( )
伽耳顿板可以演示统计规律.如图,让大量小球从上方漏斗形入口落下,最终小球都落在槽内.重复多次实验后发现( )| A. | 某个小球落在哪个槽是有规律的 | |
| B. | 大量小球在槽内的分布是无规律的 | |
| C. | 大量小球落入槽内后均匀分布在各槽中 | |
| D. | 越接近漏斗形入口处的槽内,小球聚集越多 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
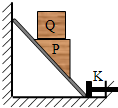 如图,刚性板放在竖直墙壁和挡板K之间,竖直墙壁和水平面光滑,物体P、Q静止叠放在板上,此时物体P的上表面水平.若将K往右缓慢移动一小段距离后重新固定,整个装置在新的位置仍保持静止,与原来的相比( )
如图,刚性板放在竖直墙壁和挡板K之间,竖直墙壁和水平面光滑,物体P、Q静止叠放在板上,此时物体P的上表面水平.若将K往右缓慢移动一小段距离后重新固定,整个装置在新的位置仍保持静止,与原来的相比( )| A. | P对板的压力减小 | B. | P对Q的支持力减小 | ||
| C. | 板对P的作用力减小 | D. | 水平地面受到的弹力减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
| 额定车速 | 整车质量 | 载重 | 额定输出功率 | 电动机额定工作电压和电流 |
| 18km/h | 40kg | 80kg | 180W | 36V/6A |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
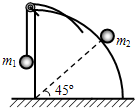 如图所示,光滑水平面上,有一$\frac{1}{4}$的球体,球体的左侧面也光滑.质量分别为m1、m2的物体(均可看作质点),通过柔软光滑的轻绳连接,与球体一起以共同的速度v0向左匀速运动,此时m2与球心O的连线与水平线成45°.m2与球面间的动摩擦因数为0.5,设m2与球面间的最大静摩擦力等于滑动摩擦力,则$\frac{m_2}{m_1}$的最小值是( )
如图所示,光滑水平面上,有一$\frac{1}{4}$的球体,球体的左侧面也光滑.质量分别为m1、m2的物体(均可看作质点),通过柔软光滑的轻绳连接,与球体一起以共同的速度v0向左匀速运动,此时m2与球心O的连线与水平线成45°.m2与球面间的动摩擦因数为0.5,设m2与球面间的最大静摩擦力等于滑动摩擦力,则$\frac{m_2}{m_1}$的最小值是( )| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com