
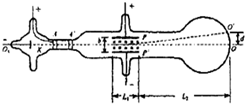
 电子的发现揭开了人类对原子结构的认识.汤姆生用来测定电子的比荷的实验装置如图所示.真空管内的阴极K发出的电子(不计初速度、重力和电子间的相互作用),经加速电压加速后,穿过A′中心的小孔沿中心轴O1O的方向进入到两块水平正对放置的平行极板P和P′间的区域.
电子的发现揭开了人类对原子结构的认识.汤姆生用来测定电子的比荷的实验装置如图所示.真空管内的阴极K发出的电子(不计初速度、重力和电子间的相互作用),经加速电压加速后,穿过A′中心的小孔沿中心轴O1O的方向进入到两块水平正对放置的平行极板P和P′间的区域.分析 (1)加偏转电压后,板间电场为匀强电场,根据匀强电场的场强公式求解
(2)当电子受到电场力与洛伦兹力平衡时,做匀速直线运动,因此由电压、磁感应强度可求出运动速度.
(3)电子在电场中做类平抛运动,将运动分解成沿电场强度方向与垂直电场强度方向,然后由运动学公式求解.电子离开电场后,做匀速直线运动,从而可以求出偏转距离的表达式,变型得到电子的荷质比表达式.
解答 解:(1)加偏转电压U后,板间区域的电场强度大小$E=\frac{U}{b}$
电场强度的方向竖直向下
(2)当电子受到的电场力与洛沦兹力平衡时,电子做匀速直线运动,亮点重新回复到中心O点,设电子的速度为v,则
evB=eE
得 v=$\frac{E}{B}$
即 $v=\frac{U}{Bb}$
(3)当极板间仅有偏转电场 时,电子以速度v进入后,竖直方向作匀加速运动,加速度为a=$\frac{eU}{mb}$
电子在水平方向作匀速运动,在电场内的运动时间为${t}_{1}^{\;}=\frac{{L}_{1}^{\;}}{v}$
这样,电子在电场中,竖直向上偏转的距离为 ${d}_{1}^{\;}=\frac{1}{2}a{t}_{1}^{2}=\frac{1}{2}×\frac{eU}{mb}×\frac{{L}_{1}^{2}}{{v}_{\;}^{2}}=\frac{eU{L}_{1}^{2}}{2mb{v}_{\;}^{2}}$
离开电场时竖直向上的分速度为 ${v}_{1}^{\;}=a{t}_{1}^{\;}=\frac{eU{L}_{1}^{\;}}{mvb}$
电子离开电场后做匀速直线运动,经t2时间到达荧光屏 ${t}_{2}^{\;}=\frac{{L}_{2}^{\;}}{v}$
t2时间内向上运动的距离为 ${d}_{2}^{\;}={v}_{1}^{\;}{t}_{2}^{\;}=\frac{eU{L}_{1}^{\;}{L}_{2}^{\;}}{m{v}_{\;}^{2}b}$
这样,电子向上的总偏转距离为$d={d}_{1}^{\;}+{d}_{2}^{\;}=\frac{eU{L}_{1}^{\;}}{2m{v}_{\;}^{2}b}(2{L}_{2}^{\;}+{L}_{1}^{\;})$
可解得 $\frac{e}{m}=\frac{2Ud}{{B}_{\;}^{2}b{L}_{1}^{\;}({L}_{1}^{\;}+2{L}_{2}^{\;})}$
答:(1)加偏转电压U后,板间区域的电场强度大小$\frac{U}{b}$和方向竖直向下;
(2)再加入磁场后,分析电子重新回到O点的原因,打在O点的电子速度的大小$\frac{U}{Bb}$;
(3)根据实验现象和条件,推导电子比荷的表达式$\frac{2Ud}{{B}_{\;}^{2}b{L}_{1}^{\;}({L}_{1}^{\;}+2{L}_{2}^{\;})}$
点评 考查平抛运动处理规律:将运动分解成相互垂直的两方向运动,因此将一个复杂的曲线运动分解成两个简单的直线运动,并用运动学公式来求解.


科目:高中物理 来源: 题型:选择题
| A. | v=9 m/s,a=3 m/s2 | B. | v=15 m/s,a=3 m/s2 | ||
| C. | v=9 m/s,a=0 | D. | v=15 m/s,a=0 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 研究共点力的合成实验中,橡皮筋一端固定在A点,用两只弹簧测力计通过细绳互成角度地拉橡皮筋,使橡皮筋的另一端伸长到O点,分别记下显示弹簧测力计拉力F1、F2方向的位置M、N(如图所示)和弹簧测力计示数F1=1.5N,F2=2.0N,再用一个弹簧测力计拉弹簧,使橡皮筋仍伸长到O点,记下弹簧测力计示数为F=2.5N,试在图上作出F1、F2和F,并验证平行四边形法则是否正确.
研究共点力的合成实验中,橡皮筋一端固定在A点,用两只弹簧测力计通过细绳互成角度地拉橡皮筋,使橡皮筋的另一端伸长到O点,分别记下显示弹簧测力计拉力F1、F2方向的位置M、N(如图所示)和弹簧测力计示数F1=1.5N,F2=2.0N,再用一个弹簧测力计拉弹簧,使橡皮筋仍伸长到O点,记下弹簧测力计示数为F=2.5N,试在图上作出F1、F2和F,并验证平行四边形法则是否正确.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
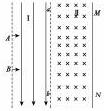
 如图所示的空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种分界线,图中虚线为磁场区的右边界,现有一质量为m、带电量为-q的带电粒子(不计重力),从电场中P点以初速度v0沿x轴正方向运动.已知P点的坐标为(-L,0),且L=$\frac{mvθ}{Eq}$.试求:
如图所示的空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种分界线,图中虚线为磁场区的右边界,现有一质量为m、带电量为-q的带电粒子(不计重力),从电场中P点以初速度v0沿x轴正方向运动.已知P点的坐标为(-L,0),且L=$\frac{mvθ}{Eq}$.试求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,真空室内竖直条形区域Ⅰ内存在竖直向下的匀强电场,条形区域Ⅱ内有垂直纸面向里的匀强磁场,磁场和电场宽度均为L且足够长,MN为涂有荧光物质的竖直板.现有质量均为m,电量大小均为q的正、负两种带电粒子,负粒子从A点、正粒子从B点以相同速度v同时在纸面内以垂直电场线方向射入电场,A、B两点间距离为$\frac{L}{2}$,已知粒子到达Ⅰ、Ⅱ区域分界面ab上时相距为$\frac{3}{2}$L,粒子射出磁场垂直打到荧光屏上,观察到两个亮斑,(不计两粒子间的相互作用)求:
如图所示,真空室内竖直条形区域Ⅰ内存在竖直向下的匀强电场,条形区域Ⅱ内有垂直纸面向里的匀强磁场,磁场和电场宽度均为L且足够长,MN为涂有荧光物质的竖直板.现有质量均为m,电量大小均为q的正、负两种带电粒子,负粒子从A点、正粒子从B点以相同速度v同时在纸面内以垂直电场线方向射入电场,A、B两点间距离为$\frac{L}{2}$,已知粒子到达Ⅰ、Ⅱ区域分界面ab上时相距为$\frac{3}{2}$L,粒子射出磁场垂直打到荧光屏上,观察到两个亮斑,(不计两粒子间的相互作用)求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
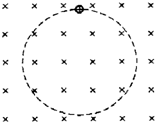 如图所示,带正电量为q的液滴,处在水平方向的匀强磁场中,磁感应强度为B,液滴运动速度为v,若要液滴在竖直平面内做半径为R的匀速圆周运动,则:
如图所示,带正电量为q的液滴,处在水平方向的匀强磁场中,磁感应强度为B,液滴运动速度为v,若要液滴在竖直平面内做半径为R的匀速圆周运动,则:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 通电线圈受到的磁力矩与电流成正比 | |
| B. | 线圈受到的弹簧的反力矩与线圈转过的角度成正比 | |
| C. | 线圈内通过的电流方向改变时,线圈转动方向仍不变 | |
| D. | 电流增大时线圈转动的角度不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 一质量为m=40kg的小孩站在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.求在这段时间内电梯上升的高度是多少(取重力加速度g=10m/s2)
一质量为m=40kg的小孩站在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.求在这段时间内电梯上升的高度是多少(取重力加速度g=10m/s2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com