
| A. | 每颗星做圆周运动的半径为$\frac{1}{2}$L | |
| B. | 每颗星做圆周运动的向心力为$\frac{{({1+\sqrt{2}})G{m^2}}}{{2{L^2}}}$ | |
| C. | 每颗星表面的重力加速度为$\frac{Gm}{R^2}$ | |
| D. | 每颗星做圆周运动的周期为$2π\sqrt{\frac{{\sqrt{2}{L^3}}}{{(1+2\sqrt{2})Gm}}}$ |
分析 星体做匀速圆周运动的轨道半径等于正方形对角线的一半.
根据万有引力等于重力求出星体表面的重力加速度.
在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力,列出等式求出星体匀速圆周运动的周期.
解答 解:A、由星体均围绕正方形对角线的交点做匀速圆周运动可知,星体做匀速圆周运动的轨道半径
r=$\frac{\sqrt{2}}{2}$L,故A错误;
B、星体在其他三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动,由万有引力定律和向心力公式得:
F合=$\frac{{Gm}^{2}}{{(\sqrt{2}L)}^{2}}$+2$\frac{{Gm}^{2}}{{L}^{2}}$cos45°=m$\frac{{4π}^{2}}{{T}^{2}}$×$\frac{\sqrt{2}}{2}$L
T=$2π\sqrt{\frac{{\sqrt{2}{L^3}}}{{(1+2\sqrt{2})Gm}}}$,故B错误,D正确;
C、根据万有引力等于重力得:$\frac{Gmm′}{{R}^{2}}$=m′g
解得:g=$\frac{Gm}{R^2}$,故C正确;
故选:CD.
点评 解决本题的关键掌握万有引力等于重力$\frac{Gmm′}{{R}^{2}}$=m′g,以及知道在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:多选题
| A. | 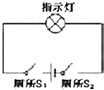 | B. | 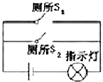 | C. | 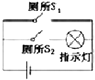 | D. | 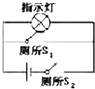 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{2L}{g{t}^{2}cosα}$-tanα,t$\sqrt{\frac{L}{g{t}^{2}sinα-L}}$ | B. | $\frac{Lcosα}{g{t}^{2}}$-tanα,t$\sqrt{\frac{gL}{{t}^{2}sinα-L}}$ | ||
| C. | $\frac{Lsinα}{{t}^{2}}$-cosα,t$\sqrt{\frac{gL}{{t}^{2}cosα-L}}$ | D. | $\frac{Ltanα}{g{t}^{2}}$-cosα,t$\sqrt{\frac{2gL}{g{t}^{2}-L}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 光是一种电磁波 | |
| B. | 电磁波是由麦克斯韦通过实验发现的 | |
| C. | 电磁波可以传递能量 | |
| D. | 电磁波的传播一定需要介质 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 牛顿总结出了万有引力定律并测出了引力常量,被后人称为称出地球的第一人 | |
| B. | 伽利略总结出太阳系行星运动的三大规律 | |
| C. | 亚里士多德通过理想实验提出力并不是维持物体运动的原因 | |
| D. | 胡克认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
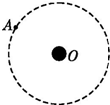 经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B运动轨道半径R( )
经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B运动轨道半径R( )| A. | R=R0$\root{3}{\frac{{{t}_{0}}^{2}}{({t}_{0}-{T}_{0})^{2}}}$ | B. | R=R0$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$ | ||
| C. | R=R0$\root{3}{\frac{({t}_{0}+{T}_{0})^{2}}{({t}_{0}-{T}_{0})^{2}}}$ | D. | R=R0$\root{3}{\frac{{t}_{0}}{{t}_{0}-{T}_{0}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 整个下落过程系统机械能减少 | |
| B. | t=0到t=32s之间,处于完全失重状态 | |
| C. | t=32s启动小伞之后,跳伞员受到的空气阻力大于重力 | |
| D. | t=41s时刻速度和加速度都最大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
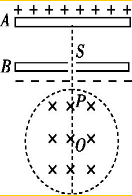 如图所示,一对带电平行金属板A、B水平放置,上下两极板间的电势差U=104V,两板间距d=10-2m,B板中央开有小孔S;金属板正下方有一半径R=10-2m的圆形的匀强磁场区域,磁场方向垂直于纸面向里,磁感应强度的大小B=1T,磁场区域的圆心O位于小孔正下方.SO连线交圆的边界于P点.比荷$\frac{q}{m}$=5×107C/kg的带正电粒子以速度v=5×105m/s从磁场外某处正对着圆心射向磁场区域,经过磁场的偏转作用,恰好沿着OP方向从小孔S进入电场.带电粒子在SP间运动的时间忽略不计,带电粒子的重力不计.求:
如图所示,一对带电平行金属板A、B水平放置,上下两极板间的电势差U=104V,两板间距d=10-2m,B板中央开有小孔S;金属板正下方有一半径R=10-2m的圆形的匀强磁场区域,磁场方向垂直于纸面向里,磁感应强度的大小B=1T,磁场区域的圆心O位于小孔正下方.SO连线交圆的边界于P点.比荷$\frac{q}{m}$=5×107C/kg的带正电粒子以速度v=5×105m/s从磁场外某处正对着圆心射向磁场区域,经过磁场的偏转作用,恰好沿着OP方向从小孔S进入电场.带电粒子在SP间运动的时间忽略不计,带电粒子的重力不计.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
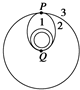 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )| A. | 在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度 | |
| B. | 在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度 | |
| C. | 在轨道3上的速率大于在轨道1上的速率 | |
| D. | 在轨道3上的角速度小于在轨道1上的角速度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com