
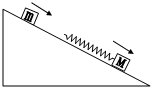
 质量m和M的两木块分别以v1和v2的速度沿粗糙足够长的斜面匀速下滑.已知斜面固定,v1>v2.求两木块发生相互作用的过程中.轻质弹簧能达到的最大弹性势能.
质量m和M的两木块分别以v1和v2的速度沿粗糙足够长的斜面匀速下滑.已知斜面固定,v1>v2.求两木块发生相互作用的过程中.轻质弹簧能达到的最大弹性势能. 分析 两木块发生相互作用的过程中,系统所受的合外力为零,系统的动量守恒,当两者速度相等时,弹簧的压缩量最大,弹簧弹性势能最大,应用动量守恒定律与能量守恒定律求出最大弹性势能.
解答 解:将两物块视为系统时,系统遵循动量守恒.且两物块速度相等时,轻质弹簧达到的弹性势能最大,以平行于斜面向下为正方向,由动量守恒定律得:mv1+Mv2=(m+M)v,
由能量守恒定律得:Epm=$\frac{1}{2}$mv12+$\frac{1}{2}$Mv22-$\frac{1}{2}$(m+M)v2,
联立方程解得,弹簧能达到的最大弹性势能:Epm=$\frac{1}{2}$mv12+$\frac{1}{2}$Mv22-$\frac{(m{v}_{1}+M{v}_{2})^{2}}{2(m+M)}$
答:弹簧能达到的最大弹性势能为$\frac{1}{2}$mv12+$\frac{1}{2}$Mv22-$\frac{(m{v}_{1}+M{v}_{2})^{2}}{2(m+M)}$.
点评 本题要分析清楚两木块运动过程,判断出系统的合外力为零,系统的动量守恒,应用动量守恒定律与能量守恒定律即可正确解题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中物理 来源: 题型:选择题
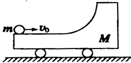 带有$\frac{1}{4}$光滑圆弧轨道,质量为M的滑车静止置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上滑车,当小球上行再返回并脱离滑车时,以下说法正确的是( )
带有$\frac{1}{4}$光滑圆弧轨道,质量为M的滑车静止置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上滑车,当小球上行再返回并脱离滑车时,以下说法正确的是( )| A. | 小球一定水平向左做平抛运动 | B. | 小球可能水平向左做平抛运动 | ||
| C. | 小球不可能做自由落体运动 | D. | 小球不可能水平向右做平抛运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离.假定空气阻力可忽略,运动员可视为质点,从绳子绷紧到运动员下落至最低点的过程中,下列说法不正确的是( )
一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离.假定空气阻力可忽略,运动员可视为质点,从绳子绷紧到运动员下落至最低点的过程中,下列说法不正确的是( )| A. | 运动员的动能先增大后减小 | |
| B. | 运动员克服弹力做功,蹦极绳弹性势能增加 | |
| C. | 运动员重力势能始终减小 | |
| D. | 重力势能的改变量与重力势能零点的选取有关 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 月球表面的重力加速度 | B. | 月球的质量 | ||
| C. | 月球的第一宇宙速度 | D. | 月球对宇航员的引力 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
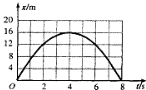 一物体从某行星表面竖直向上抛出.从抛出瞬间开始计时物体相对于抛出点的位移x与所用时间t的关系如图所示.已知该星球半径R=8×105Km,万有引力常G=6.67×10-11N.m2/kg2,由图可知( )
一物体从某行星表面竖直向上抛出.从抛出瞬间开始计时物体相对于抛出点的位移x与所用时间t的关系如图所示.已知该星球半径R=8×105Km,万有引力常G=6.67×10-11N.m2/kg2,由图可知( )| A. | 该行星表面的重力加速度大小为2m/s2 | |
| B. | 该行星质量的数量级为1020Kg | |
| C. | 物体抛出时的初速度大小为8m/s | |
| D. | 该行星的第一宇宙速度为V1=50km/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 在不同的惯性参考系中,物理定律的数学形式是不同的 | |
| B. | 真空中的光速在不同惯性参考系中不相同的 | |
| C. | 一条沿身长度方向高速运动的杆子,其长度与静止时不同 | |
| D. | 一条沿垂直于自身长度的方向高速运动杆子,其长度与静止时不同 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 小球落地点与抛出点的水平距离为9.8m | |
| B. | 小球落地点与抛出点的水平距离为4.9m | |
| C. | 小球落地时的速度大小为4.9m/s | |
| D. | 小球落地时的速度大小为9.8m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
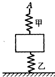 如图所示,物块质量为m,与甲、乙两弹簧相连接,乙弹簧下端与地面连接,甲、乙两弹簧质量不计,其劲度系数分别为k1、k2,起初甲弹簧处于自由长度,现用手将甲弹簧的A端缓慢上提,使乙弹簧产生的弹力大小变为原来的$\frac{2}{3}$,则A端上移距离可能是( )
如图所示,物块质量为m,与甲、乙两弹簧相连接,乙弹簧下端与地面连接,甲、乙两弹簧质量不计,其劲度系数分别为k1、k2,起初甲弹簧处于自由长度,现用手将甲弹簧的A端缓慢上提,使乙弹簧产生的弹力大小变为原来的$\frac{2}{3}$,则A端上移距离可能是( )| A. | $\frac{{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | B. | $\frac{2{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | ||
| C. | $\frac{4{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | D. | $\frac{5{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com