
 ��ͼ����ʾ��һ�������Ƶľ���ϵ��Ϊk���ᵯ���϶˹̶����¶�����һ����Ϊm����飬����һ����ΪM����������ѹ�����ɣ���ͼ����ʾ��������ͻȻ����ʱ���������µļ��ٶȣ����СΪa��a��g���������һ���������������ϣ�ʹ���̺���鹲ͬ������$\frac{a}{3}$�ļ��ٶ����ȼ���ֱ���˶�����
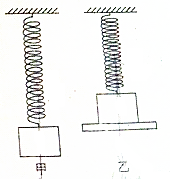
��ͼ����ʾ��һ�������Ƶľ���ϵ��Ϊk���ᵯ���϶˹̶����¶�����һ����Ϊm����飬����һ����ΪM����������ѹ�����ɣ���ͼ����ʾ��������ͻȻ����ʱ���������µļ��ٶȣ����СΪa��a��g���������һ���������������ϣ�ʹ���̺���鹲ͬ������$\frac{a}{3}$�ļ��ٶ����ȼ���ֱ���˶��������� ��1��������ͻȻ����ʱ���������µļ��ٶȣ����СΪa�������壬��ţ�ٵڶ����ɵõ��ɵ��쳤������ľ���������Ҫ����ʱ������֮��ĵ���Ϊ�㣬����ţ�ٵڶ��������������շ���ʱ�����쳤�ij��ȣ����ɵ��쳤�ij��ȵ��������λ�ƣ���λ�ƹ�ʽ���ʱ�䣮
��2�������������������Գ�ĩ״̬������������ţ���˶�����������Ĵ�С��
��� �⣺������ͻȻ����ʱ���������µļ��ٶȣ����СΪa�������壬��ţ�ٵڶ����ɵã�
mg+F=ma
�� F=kx1��
�ã�x1=$\frac{m��a-g��}{k}$
��ľ�������弴������ʱ��m����������N=0�������壬��ţ�ٵڶ����ɵã�
mg-F��=m$•\frac{a}{3}$
�� F��=kx��2��
�ɣ�x2=$\frac{m��g-\frac{1}{3}a��}{k}$
����λ��ʱ���ϵ֪x1+x2=$\frac{1}{2}$$•\frac{1}{3}a$t2 �ã�
t=$\sqrt{\frac{2��{x}_{1}+{x}_{2}��}{\frac{a}{3}}}$=2$\sqrt{\frac{m}{k}}$
��2����������������֪��״̬��M+m��g+F-F1=��M+m��•$\frac{1}{3}a$
��ϣ�1�����F1=M��g-$\frac{1}{3}a$��$+\frac{2}{3}a$m
��������������֪��״̬��M+m��g+F��-F2=��M+m��•$\frac{1}{3}a$
��ϣ�1�����F2=Mg-$\frac{1}{3}Ma$
��
��1�����߹�ͬ���ȼ���ֱ���˶���ʱ��Ϊ2$\sqrt{\frac{m}{k}}$��
��2�����˶������п�ʼ����ֹ˲�������Ĵ�С�ֱ�ΪM��g-$\frac{1}{3}a$��$+\frac{2}{3}a$��Mg-$\frac{1}{3}Ma$��
���� ����ؼ���������շ���ʱ�ٽ�����������Ϊ�㣮ţ�ٵڶ������о�ijһ״̬ʱ����ĺ�������ٶȵĹ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
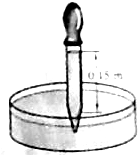 һ���ιܣ���β������һ�����������ȰѵιܵIJ��������ˮ�У�Ȼ���ѹ�ͷ�����ʹˮ����ι��ڲ���ͼ�еι��ڲ���Һ��ߴ������ڵ�Һ��0.15m����ô�����������ѹǿ�Ƕ��٣������ѹp0=1.0��105Pa�������������װ���Ƶ���ɽ�ϣ��ι���ˮ��Ч����ʲô�仯��Ϊʲô��
һ���ιܣ���β������һ�����������ȰѵιܵIJ��������ˮ�У�Ȼ���ѹ�ͷ�����ʹˮ����ι��ڲ���ͼ�еι��ڲ���Һ��ߴ������ڵ�Һ��0.15m����ô�����������ѹǿ�Ƕ��٣������ѹp0=1.0��105Pa�������������װ���Ƶ���ɽ�ϣ��ι���ˮ��Ч����ʲô�仯��Ϊʲô���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��ֹ��������Ƶ� | B�� | ������������Ƶ� | ||
| C�� | ������������� | D�� | �������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 1932�꣬����˹������˹��Ƴ��˻����������������������Ĺ���ԭ����ͼ��ʾ�����ڸ�����е�D�ν����а뾶ΪR�����м�������С���������Ӵ�����ʱ����Ժ��Բ��ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ��A������Դ���������ӣ�����Ϊm�������Ϊ+q���ڼ��ٵ�ѹΪU�ļ������б����٣����ٹ����в����������ЧӦ���������ã��������ӵij��ٶȣ�
1932�꣬����˹������˹��Ƴ��˻����������������������Ĺ���ԭ����ͼ��ʾ�����ڸ�����е�D�ν����а뾶ΪR�����м�������С���������Ӵ�����ʱ����Ժ��Բ��ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ��A������Դ���������ӣ�����Ϊm�������Ϊ+q���ڼ��ٵ�ѹΪU�ļ������б����٣����ٹ����в����������ЧӦ���������ã��������ӵij��ٶȣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��ˮƽ���õ�����A���ݻ�ΪVB=3.6L������B����һ�ݻ��ɺ��Բ��Ƶij�ϸ�ܾ�����C����������A����һ����D����������Ħ�����������ڻ�����A�����¶Ⱥ�ΪT1=300K��ѹǿΪp0=1.0��105Pa�Ĵ����У�B����T2=400K�ĺ��²��ڣ�B�����ڵ����������ã���ʼʱC�ǹرյģ�A��װ���¶�ΪT1=300K�����ΪVA=2.4L�����壬B��û�����壬����C��ʹ������A����B���ȵ�����Dֹͣ�ƶ�һ��ʱ����������������������������ѹǿ��
��ͼ��ʾ��ˮƽ���õ�����A���ݻ�ΪVB=3.6L������B����һ�ݻ��ɺ��Բ��Ƶij�ϸ�ܾ�����C����������A����һ����D����������Ħ�����������ڻ�����A�����¶Ⱥ�ΪT1=300K��ѹǿΪp0=1.0��105Pa�Ĵ����У�B����T2=400K�ĺ��²��ڣ�B�����ڵ����������ã���ʼʱC�ǹرյģ�A��װ���¶�ΪT1=300K�����ΪVA=2.4L�����壬B��û�����壬����C��ʹ������A����B���ȵ�����Dֹͣ�ƶ�һ��ʱ����������������������������ѹǿ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | С���Ĺ��Ա�� | B�� | С������ʧ��״̬ | ||
| C�� | С�����ڳ���״̬ | D�� | С���Ļ�е���غ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com