
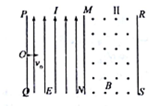
 如图所示,在Ⅰ区里有竖直方向的匀强电场E=4×105N/C,在Ⅱ区里有垂直于纸面向外的匀强磁场,电场竖直边界PQ、MN的间距和磁场竖直边界MN、RS的间距相等均为d,d=0.4m.质荷比$\frac{m}{q}$=4×10-10kg/C的带正电粒子,以初速度v0=2×107m/s从PQ边界上的O点垂直PQ射入电场.若电、磁场在竖直方向分布足够广,不计粒子的重力.求;
如图所示,在Ⅰ区里有竖直方向的匀强电场E=4×105N/C,在Ⅱ区里有垂直于纸面向外的匀强磁场,电场竖直边界PQ、MN的间距和磁场竖直边界MN、RS的间距相等均为d,d=0.4m.质荷比$\frac{m}{q}$=4×10-10kg/C的带正电粒子,以初速度v0=2×107m/s从PQ边界上的O点垂直PQ射入电场.若电、磁场在竖直方向分布足够广,不计粒子的重力.求;分析 (1)由类平抛运动规律求得运动时间,再根据受力求得加速度,即可求得竖直分速度,进而由速度的合成求得速度大小及方向;
(2)根据几何关系求得半径范围,然后由洛伦兹力做向心力求得磁感应强度范围;
(3)根据几何关系求得粒子在磁场中转过的中心角及粒子再次进入电场时水平分速度,然后由匀速圆周运动规律及类平抛运动规律求得运动时间.
解答 解:(1)粒子在电场中运动只受电场力作用,做类平抛运动,故运动时间${t}_{1}=\frac{d}{{v}_{0}}=2×1{0}^{-8}s$,粒子运动的加速度$a=\frac{qE}{m}=1×1{0}^{15}m/{s}^{2}$;
故粒子经过电场、磁场边界MN时的竖直分速度${v}_{y}=a{t}_{1}=2×1{0}^{7}m/s$,速度$v=\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=2\sqrt{2}×1{0}^{7}m/s$,与v0方向的夹角$θ=arctan\frac{{v}_{y}}{{v}_{0}}=45°$;
(2)若要粒子不从RS穿出,那么,由几何关系可得:粒子在磁场中做圆周运动的半径$R≤\frac{d}{1+sin45°}=0.4(2-\sqrt{2})m$;
故由洛伦兹力做向心力可得:$Bvq=\frac{m{v}^{2}}{R}$,所以,$B=\frac{mv}{qR}≥0.02(1+\sqrt{2})T$;
(3)由粒子在磁场中做圆周运动,根据几何关系可知:粒子在磁场中转过$\frac{3}{2}π$的中心角,粒子离开磁场时在MN上速度沿水平方向的分量为v0;
所以,粒子在电场中运动时间${t}_{1}′=2×\frac{d}{{v}_{0}}=4×1{0}^{-8}s$;粒子在磁场中的运动时间${t}_{2}=\frac{3}{4}T=\frac{3}{4}×\frac{2πR}{v}≤3π(\sqrt{2}-1)×1{0}^{-8}s$=3.9×10-8s;
所以,粒子在电、磁场中的运动时间的最大可能值为${t}_{1}′+{t}_{2m}=7.9×1{0}^{-8}s$;
答:(1)粒子经过电场、磁场边界MN时的速度为$2\sqrt{2}×1{0}^{7}m/s$,偏离v0方向的夹角为45°;
(2)若要使粒子未从磁场边界RS穿出,则磁感应强度B的取值范围为$B≥0.02(1+\sqrt{2})T$;
(3)粒子在电、磁场中的运动时间的最大可能值为7.9×10-8s.
点评 带电粒子的运动问题,加速电场一般由动能定理或匀加速运动规律求解;偏转电场由类平抛运动规律求解;磁场中的运动问题则根据圆周运动规律结合几何条件求解.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中物理 来源: 题型:计算题
 2017年1月25日,在中央电视台播出的“2016年度科技盛典”节目,海军电力工程专家马伟明院士表示正在研制“国产003型航母电磁弹射器”(如图所示),它是由电磁弹射车给飞机一个辅助作用力,使飞机在较短的直跑道上获得较大的速度,假定航母处于静止状态,质量为M的飞机利用电磁弹射器起飞,飞机在t0时刻从静止开始在跑道上作匀加速运动,在t1时刻获得发射速度v,此过程中飞机发电机的推力恒为F,阻力恒为f,问:
2017年1月25日,在中央电视台播出的“2016年度科技盛典”节目,海军电力工程专家马伟明院士表示正在研制“国产003型航母电磁弹射器”(如图所示),它是由电磁弹射车给飞机一个辅助作用力,使飞机在较短的直跑道上获得较大的速度,假定航母处于静止状态,质量为M的飞机利用电磁弹射器起飞,飞机在t0时刻从静止开始在跑道上作匀加速运动,在t1时刻获得发射速度v,此过程中飞机发电机的推力恒为F,阻力恒为f,问:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
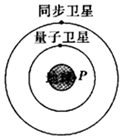 我国首颗量子科学实验卫星于2016年8月16日1点40分成功发射.量子卫星成功运行后,我国将在世界上首次实现卫星和地面之间的量子通信,构建天地一体化的量子保密通信与科学实验体系.假设量子卫星轨道在赤道平面,如图所示.已知量子卫星的轨道半径是地球半径的m倍,同步卫星的轨道半径是地球半径的n倍,图中P点是地球赤道上一点,由此可知( )
我国首颗量子科学实验卫星于2016年8月16日1点40分成功发射.量子卫星成功运行后,我国将在世界上首次实现卫星和地面之间的量子通信,构建天地一体化的量子保密通信与科学实验体系.假设量子卫星轨道在赤道平面,如图所示.已知量子卫星的轨道半径是地球半径的m倍,同步卫星的轨道半径是地球半径的n倍,图中P点是地球赤道上一点,由此可知( )| A. | 同步卫星与量子卫星的运行周期之比为$\frac{{n}^{3}}{{m}^{3}}$ | |
| B. | 同步卫星与P点的速率之比为$\sqrt{\frac{1}{n}}$ | |
| C. | 量子卫星与P点的速率之比为$\sqrt{\frac{{n}^{3}}{m}}$ | |
| D. | 量子卫星与同步卫星的速率之比为$\frac{n}{m}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在真空中A、B两点分别放在异种点电荷-Q和+2Q,以AB连线中点O为圆心作一圆形路径abcd,如图所示,则下列说法正确的是( )
在真空中A、B两点分别放在异种点电荷-Q和+2Q,以AB连线中点O为圆心作一圆形路径abcd,如图所示,则下列说法正确的是( )| A. | 场强大小关系有Ea=Eb、Ec=Ed | |
| B. | 电势高低关系有φa>φb、φc=φd | |
| C. | 将一负点电荷沿圆弧由a运动到b的过程中电场力做正功 | |
| D. | 将一正点电荷沿直线由c运动到d的过程中电势能始终不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 某同学在青少年科技创新活动中设计了一个简易火灾报警装置,其原理如图所示,竖直放置的试管中装有水银,当温度升高时,水银柱上升,使电路导通,蜂鸣器发出报警的响声,27℃时,空气柱长度L1为20cm,水银上表面与导线下端的距离L2为10cm,管内水银柱的高度h为4cm,大气压强为76cmHg.
某同学在青少年科技创新活动中设计了一个简易火灾报警装置,其原理如图所示,竖直放置的试管中装有水银,当温度升高时,水银柱上升,使电路导通,蜂鸣器发出报警的响声,27℃时,空气柱长度L1为20cm,水银上表面与导线下端的距离L2为10cm,管内水银柱的高度h为4cm,大气压强为76cmHg.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 一粗糙的水平传送带以恒定的速率v1沿顺时针运动,传送带的左、右两端皆有一与传送带等高的光滑水平面,质量为m的物体以相同的速率v2分别从左右两端滑上传送带且从另一端滑出,下列说法正确的是( )
一粗糙的水平传送带以恒定的速率v1沿顺时针运动,传送带的左、右两端皆有一与传送带等高的光滑水平面,质量为m的物体以相同的速率v2分别从左右两端滑上传送带且从另一端滑出,下列说法正确的是( )| A. | 物体两次通过传送带的时间可能相等 | |
| B. | 物体两次通过传送带的时间可能不相等 | |
| C. | 若物体在传送带上均一直做减速运动,则两次运动物体与传送带间摩擦生热相等 | |
| D. | 若物体在传送带上均一直做减速运动,则两次运动物体与传送带间摩擦生热不相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com