

分析 根据验证机械能守恒定律的原理以及误差进行分析,选择正确的答案.
用自由落体运动运动验证机械能守恒定律,根据mgh=$\frac{1}{2}$mv2可知不需要测量重物的质量m,为保证重物做自由落体运动,必须保证计时器的两限位孔在同一竖直线上且重物的质量要大体积要小,这样才能保证物体做自由落体运动;
纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
解答 解:①AB、实验时选择质量较大的重锤,使得重力远大于阻力,使得阻力的影响可以忽略.故A正确,B错误.
CD、根据mgh=$\frac{1}{2}$mv2知,验证机械能守恒定律不一定需要测量重锤的质量,因为重力势能的减小量和动能的增加量中都含有质量,可以约去.故C正确,D错误.
故选:AC;
②根据匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度有:
v2=$\frac{{h}_{1}+{h}_{2}}{2T}$=$\frac{({h}_{1}+{h}_{2})f}{2}$
v5=$\frac{{h}_{4}+{h}_{5}}{2T}$=$\frac{({h}_{4}+{h}_{5})f}{2}$
在第2点位置时重锤的动能为:EK2=$\frac{1}{2}$mv22=$\frac{1}{8}m({h}_{1}+{h}_{2})^{2}{f}^{2}$
在第5点位置时重锤的动能为:EK5=$\frac{1}{2}$mv52=$\frac{1}{8}m({h}_{4}+{h}_{5})^{2}{f}^{2}$
重力做功等于重力势能的减小量,因此有:
重锤从第2点至第5点间的过程中重力势能的减小量为△EP=mgx25=mg(h2+h3+h4)
故答案为:①AC;②$\frac{1}{8}m({h}_{1}+{h}_{2})^{2}{f}^{2}$,$\frac{1}{8}m({h}_{4}+{h}_{5})^{2}{f}^{2}$,mg(h2+h3+h4).
点评 解决本题的关键要知道重物带动纸带下落过程中能量转化的过程和能量守恒.知道能够减小实验误差的方法;
用运动学公式、推论和动能、重力势能的定义式解决问题是该实验的常规问题,要注意单位的换算和有效数字的保留.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:选择题
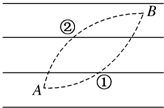 如图所示,平行直线为匀强电场中的一组电场线,有一个电荷量q=2×10-2C的正电荷仅受静电力的作用由A点沿曲线运动到B点,虚线①②是其可能运动的轨迹,已知这个运动过程中电荷的动能减少了2J,设B点电势为零,则以下说法中正确的是( )
如图所示,平行直线为匀强电场中的一组电场线,有一个电荷量q=2×10-2C的正电荷仅受静电力的作用由A点沿曲线运动到B点,虚线①②是其可能运动的轨迹,已知这个运动过程中电荷的动能减少了2J,设B点电势为零,则以下说法中正确的是( )| A. | A点的电势为100 V | B. | 电荷沿轨迹②运动 | ||
| C. | 电场强度方向向左 | D. | 电荷在A点的电势能为2 J |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
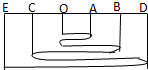 在运动场的一条直线跑道上,如图所示,每隔5m放置一个空瓶子,运动员在进行往返跑训练,从O点瓶子处出发,跑向最近的空瓶将其扳倒后再返回扳倒出发点处的第一个瓶子,之后再返到前面的最近处的瓶子,依次进行下去,当他扳倒第六个空瓶时,他跑过的路程和多大?位移是多大?方向如何?
在运动场的一条直线跑道上,如图所示,每隔5m放置一个空瓶子,运动员在进行往返跑训练,从O点瓶子处出发,跑向最近的空瓶将其扳倒后再返回扳倒出发点处的第一个瓶子,之后再返到前面的最近处的瓶子,依次进行下去,当他扳倒第六个空瓶时,他跑过的路程和多大?位移是多大?方向如何?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法运用了建立物理模型法 | |
| B. | 根据速度的定义式v=$\frac{△x}{△t}$,当△t趋近于零时,就可以表示物体在t时刻的瞬时速度,该定义运用了微元法 | |
| C. | 在实验探究加速度与力、质量的关系时,运用了科学假设法 | |
| D. | 在推导匀变速直线运动位移公式时,把整个运动过程等分成很多小段,然后将各小段位移相加,运用了极限思想法 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 根据速度定义式v=$\frac{△x}{△t}$,当△t→0时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义运用了“控制变量法” | |
| B. | 在建立合力与分力概念、合运动与分运动概念时运用了“等效替代法”的思维方法 | |
| C. | 在推导匀变速直线运动的位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,再把各小段位移相加,这里运用了微元法 | |
| D. | 物理量的定义公式:速度v=$\frac{△x}{△t}$,加速度a=$\frac{△v}{△t}$、电流强度I=$\frac{q}{t}$、物质密度ρ=$\frac{m}{V}$应用的都是“比值定义法” |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,长木板置于光滑水平地面上,小物块放在长木板的正中间,两物体处于静止状态.已知木板的质量为M=4kg,长度为L=2m,物块的质量为m=1kg,尺寸可以忽略.物块与木板之间的摩擦因数为μ=0.2,认为两物体间的最大静摩擦力和滑动摩擦力大小相等.取重力加速度g=10m/s2.
如图所示,长木板置于光滑水平地面上,小物块放在长木板的正中间,两物体处于静止状态.已知木板的质量为M=4kg,长度为L=2m,物块的质量为m=1kg,尺寸可以忽略.物块与木板之间的摩擦因数为μ=0.2,认为两物体间的最大静摩擦力和滑动摩擦力大小相等.取重力加速度g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
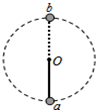 如图所示,细杆的一端与小球相连,可绕O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg,现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为Va=4m/s,小球通过轨道最高点b处的速度为Vb=1m/s,g取10m/s2.则杆对小球的作用力( )
如图所示,细杆的一端与小球相连,可绕O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg,现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为Va=4m/s,小球通过轨道最高点b处的速度为Vb=1m/s,g取10m/s2.则杆对小球的作用力( )| A. | 最高点b处为拉力,大小为24N | B. | 最高点b处为支持力,大小为24N | ||
| C. | 最低点a处为拉力,大小为96N | D. | 最低点a处为拉力,大小为66N |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com