
分析 将秒摆移到距离地面为nR0的高度处(R0为地球半径),重力加速度发生了变化,则单摆的周期也发生了变化,根据万有引力等于重力,求出重力加速度变为原来的几倍,再根据单摆的周期公式,得出周期变为原来的几倍.
解答 解:设秒摆移到距离地面为nR0的高度处的重力加速度为g′,周期为T′,则有:
$G\frac{Mm}{{{{(nRo)}^2}}}=mg'$,
在地表:$G\frac{{{m_1}{m_2}}}{{R{o^2}}}=mg$,
解得:$\frac{g'}{g}={(\frac{1}{n+1})^2}$,
由$T=2π\sqrt{\frac{l}{g}}$得:$\frac{T'}{T}=\sqrt{\frac{g}{g'}}=n+1$,
即:T′=(n+1)T=2(n+1)s.
答:秒摆的周期为2(n+1)s.
点评 解决本题的关键掌握万有引力等于重力这一理论,在空中的时候重力加速度和地面上的是不同的;其次要掌握单摆的周期公式.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:解答题
 如图所示,在直角坐标系的第Ⅰ象限和第Ⅲ象限存在着电场强度均为E的匀强电场,其中第Ⅰ象限电场沿x轴正方向,第Ⅲ象限电场沿y轴负方向.在第Ⅱ象限和第Ⅳ象限存在着匀强磁场,磁场方向均垂直纸面向里.有一个电子从y轴的P点以垂直于y轴的初速度v0进入第Ⅲ象限,第一次到达x轴上时速度方向与x轴负方向夹角为45°,第一次进入第Ⅰ象限时,与y轴正方向夹角也是45°,经过一段时间电子又回到了P点,已知电子的电荷量为e,质量为m,不考虑重力和空气阻力.求:
如图所示,在直角坐标系的第Ⅰ象限和第Ⅲ象限存在着电场强度均为E的匀强电场,其中第Ⅰ象限电场沿x轴正方向,第Ⅲ象限电场沿y轴负方向.在第Ⅱ象限和第Ⅳ象限存在着匀强磁场,磁场方向均垂直纸面向里.有一个电子从y轴的P点以垂直于y轴的初速度v0进入第Ⅲ象限,第一次到达x轴上时速度方向与x轴负方向夹角为45°,第一次进入第Ⅰ象限时,与y轴正方向夹角也是45°,经过一段时间电子又回到了P点,已知电子的电荷量为e,质量为m,不考虑重力和空气阻力.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示的电路中,U=10V,电阻R1=3Ω、R2=2Ω、R3=5Ω、电容器的电容C1=4μF、C2=1μF、求:
如图所示的电路中,U=10V,电阻R1=3Ω、R2=2Ω、R3=5Ω、电容器的电容C1=4μF、C2=1μF、求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一半径为R的光滑半圆形轨道AB固定在水平地面上,一个质量为m的小球以某一速度从半圆形轨道的最低点A冲上轨道,当小球将要从轨道最高点B飞出时,小球对轨道的压力为3mg(g为重力加速度),求:
如图所示,一半径为R的光滑半圆形轨道AB固定在水平地面上,一个质量为m的小球以某一速度从半圆形轨道的最低点A冲上轨道,当小球将要从轨道最高点B飞出时,小球对轨道的压力为3mg(g为重力加速度),求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
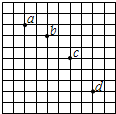 在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.
在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
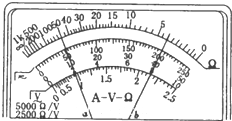 多用电表是生活实际中常用的仪器,某同学使用多用电表进行了两次测量,指针所指的位置分别如图中a、b所示.若选择开关处在“×10”的欧姆挡时指针位于a,则被测电阻的阻值是500Ω;若选择开关处在“直流电压2.5V”挡时,指针位于b,则被测电压是2.0V.
多用电表是生活实际中常用的仪器,某同学使用多用电表进行了两次测量,指针所指的位置分别如图中a、b所示.若选择开关处在“×10”的欧姆挡时指针位于a,则被测电阻的阻值是500Ω;若选择开关处在“直流电压2.5V”挡时,指针位于b,则被测电压是2.0V.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量为m1=0.2kg,大小可忽略不计的物块A以V1=3m/s的速度水平向右滑上质量为m2=0.1kg的木板B的左端,同时木板B以V2=1m/s水平向左运动,AB间动摩擦因数μ=0.5,水平面光滑,木板B的长度L=0.5m,g=10m/s2.求:从物块A滑上木板B至滑离木板B的过程中A对B的冲量大小.
如图所示,质量为m1=0.2kg,大小可忽略不计的物块A以V1=3m/s的速度水平向右滑上质量为m2=0.1kg的木板B的左端,同时木板B以V2=1m/s水平向左运动,AB间动摩擦因数μ=0.5,水平面光滑,木板B的长度L=0.5m,g=10m/s2.求:从物块A滑上木板B至滑离木板B的过程中A对B的冲量大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com