
 如题图1所示的坐标系内,在x0(x0>0)处有一垂直工轴放置的挡板.在y轴与挡板之间的区域内存在一个与xoy平珏垂直且指向纸内的匀强磁场,磁感应强度B=0.2T.位于坐标原点O处的粒子源向xoy平面内发射出大量同种带正电的粒子,所有粒子的初速度大小均为vo=1.0×106m/s,方向与x轴正方向的夹角为θ,且0≤θ≤90°.该粒子的比荷为
如题图1所示的坐标系内,在x0(x0>0)处有一垂直工轴放置的挡板.在y轴与挡板之间的区域内存在一个与xoy平珏垂直且指向纸内的匀强磁场,磁感应强度B=0.2T.位于坐标原点O处的粒子源向xoy平面内发射出大量同种带正电的粒子,所有粒子的初速度大小均为vo=1.0×106m/s,方向与x轴正方向的夹角为θ,且0≤θ≤90°.该粒子的比荷为| q | m |
| θ |
| 2π |
 解:(1)由牛顿第二定律得:qvB=m
解:(1)由牛顿第二定律得:qvB=m
| ||
| R |
| mv0 |
| qB |
| 2πR |
| v |
| 2πm |
| Bq |
| 4 |
| 3 |
| ||
| 2π |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中物理 来源: 题型:
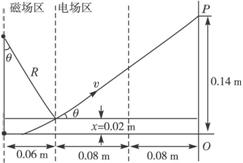
(1)定性说明电子在磁场区、电场区、无场区的运动情况。
(2)求出磁感应强度B和电场强度E的大小。(如需作图辅助解题,请在题图中作图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com