
 ������Ϊm��С��A����+q��B�����磬����ֹ���ڹ⻬ˮƽ���ϣ������l�����ڿռ���AB�����һ���糡ǿ�ȴ�СΪE����ǿ�糡��t=0ʱ�̣�A��ʼ�ܵ糡���˶�������һ��ʱ�䣬A��B���һ�η��������������������ٶȽ�����������ת�ƣ��Ժ�A��B֮�����ײ���ǵ�����ײ���������ٶ�Ϊg����
������Ϊm��С��A����+q��B�����磬����ֹ���ڹ⻬ˮƽ���ϣ������l�����ڿռ���AB�����һ���糡ǿ�ȴ�СΪE����ǿ�糡��t=0ʱ�̣�A��ʼ�ܵ糡���˶�������һ��ʱ�䣬A��B���һ�η��������������������ٶȽ�����������ת�ƣ��Ժ�A��B֮�����ײ���ǵ�����ײ���������ٶ�Ϊg�������� ��1��������ǿ�糡��A���ȼ����˶���B�Ծ�ֹ���ɶ��ܶ�����A��B��һ�θ�Ҫ������ײʱA����ٶȣ�
��2��������������ײ�����������������������ײ�����߽����ٶȣ��˺�B�������˶���A�����ٶ�Ϊ����ȼ����˶�������ţ�ٵڶ����ɺ��˶�ѧλ�ƹ�ʽ�����⣮
��3����������Ľ�����о�ÿ����ײ��Ĺ��ɣ������ӵ�1����ײ��������19����ײ��Ҫ������������ʱ�䣮
��� �⣺��1����A��ʼ�˶�����һ����ײ֮ǰ����A���ɶ��ܶ�����
qEl=$\frac{1}{2}m{v}_{1}^{2}$
�ɵ� v1=$\sqrt{\frac{2qEl}{m}}$
��2����һ�η�����ײ�������ٶȣ�A���ٶȱ�Ϊ0��B���ٶȱ�Ϊv1����С��A�ļ��ٶ�Ϊa����һ������������ڶ��η�����ײǰ˲�侭��ʱ��Ϊt2����
����ţ�ٵڶ�����֪��qE=ma
��λ��ʱ���ϵ�У�v1t2=$\frac{1}{2}a{t}_{2}^{2}$
��� t2=$\frac{2}{qE}$$\sqrt{2qElm}$
��3����ڶ��η�����ײǰA���ٶ�Ϊv2���� v2=at2=2v1��
��A��B�ڶ�����ײ���ٶȣ�B���ٶȱ�Ϊ2v1��A���ٶȱ�Ϊv1����������ײ�������v1���ٶȿ�ʼ��A������B����������ʱ����t2��ͬ���Դ����ƣ���1����������19������֮���ʱ�� t19=t18=��=t2=$\frac{2}{qE}$$\sqrt{2qElm}$
����ʱ�� t=18t2=$\frac{36}{qE}$$\sqrt{2qElm}$
��
��1��A��B��һ�θ� Ҫ������ײʱ��A����ٶ���$\sqrt{\frac{2qEl}{m}}$��
��2����A��B��һ�η�����ײ���ڶ�����ײ����ʱ��Ϊ$\frac{2}{qE}$$\sqrt{2qElm}$��
��3���ӵ�1����ײ��������19����ײ��Ҫ������������ʱ����$\frac{36}{qE}$$\sqrt{2qElm}$��
���� �����Դ��������ڵ糡�е��˶�Ϊ�������⣬�ؼ�Ҫ��ȷ������ײ��ʱ�����Ƿ���ȣ�Ȼ�����ò���ȫ���ɵķ����ó����ۣ���Ȼ����������ͼ���������ʱ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��Ħ�������Dz����� | |
| B�� | ����Ħ�������Բ����� | |
| C�� | �������岻����������һ����ֹ | |
| D�� | ������̫���˶�ʱ��̫�������ǵ�����ʼ�ղ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���ӵ��ٶȼӱ������ڼ��� | B�� | ���ӵĽ��ٶȼӱ�������뾶���� | ||
| C�� | ���ӵ����ʲ��䣬���ٶȼ��� | D�� | ���ӵ����ʲ��䣬���ڲ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
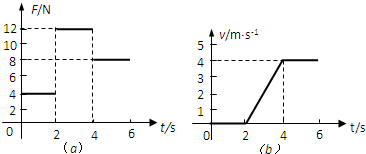
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
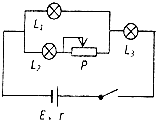
| A�� | ��·�ܵ����С��·�˵�ѹ��С����Դ�綯�Ʋ��� | |
| B�� | ��·�ܵ����С����·�������Դ������ʱ�� | |
| C�� | ��·�ܵ����С����Դ��Ч�ʱ�� | |
| D�� | L1�䰵��L2������L3Ҳ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ʵ�λ���У���ѧ��Χ�ڣ��涨�Ļ������ǣ�ǧ�ˣ��ף��� | |
| B�� | ����Ϊ6�棬���е�λ��Ϊ���ʵ�λ�е�����ѧ�¶ȵĵ�λ | |
| C�� | �������Ķ���ʽ�ǣ�B=$\frac{F}{IL}$����B�ĵ�λ��$\frac{kg}{{A{s^2}}}$ | |
| D�� | ���F=G•$\frac{{{m_i}{m_2}}}{r^2}$����ȷ�ģ����������G�ĵ�λΪ��N•$\frac{m^2}{{k{g^2}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
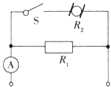 ��ͼ��ʾΪ�綯���붨ֵ����R1�����ĵ�·����·���˼ӵĵ�ѹ��ΪU����ʼS�Ͽ���������ʾ��ΪI1��S�պϺ�綯��������ת����������ʾ��ΪI2������Ϊ���������綯��������ΪR2�������й�ϵʽ��ȷ���ǣ�������
��ͼ��ʾΪ�綯���붨ֵ����R1�����ĵ�·����·���˼ӵĵ�ѹ��ΪU����ʼS�Ͽ���������ʾ��ΪI1��S�պϺ�綯��������ת����������ʾ��ΪI2������Ϊ���������綯��������ΪR2�������й�ϵʽ��ȷ���ǣ�������| A�� | $\frac{U}{{I}_{1}-{I}_{2}}$=R2 | B�� | $\frac{U}{{I}_{2}}$=$\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}$ | ||
| C�� | I2U=$\frac{{U}^{2}}{{R}_{1}}$+$\frac{{U}^{2}}{{R}_{2}}$ | D�� | I2U=��I1-I2��U+I22R1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ٤�����о����������˶�ʱ�����������Ѱ�����ȷ��������ʱ�� | |
| B�� | ţ�ٵ�һ������ʵ�鶨�� | |
| C�� | ����ʿ�����Ϊ������˶�����Ҫ����ά�� | |
| D�� | ţ�ٵ�һ����˵�����Ǹı������˶�״̬��ԭ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com