
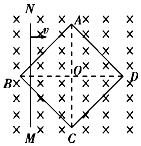
 ��ͼ�������αպ� �����ABCD�ɴ�ϸ���ȵ�ͬ�ֲ����Ƴɣ�����ͬ�����ƳɵĽ�����MN�������ε��߿�ĶԽ��߳���ǡ����ȣ����߿��������ǿ�ų��У��ų��ĴŸ�Ӧǿ�ȷ���ֱ���߿�����ƽ�����������MN�뵼�߿�Ӵ����ã��ҵ��߿�Խ���BD��ֱƽ��MN����������B�����������˶���AC�Ĺ����У�������
��ͼ�������αպ� �����ABCD�ɴ�ϸ���ȵ�ͬ�ֲ����Ƴɣ�����ͬ�����ƳɵĽ�����MN�������ε��߿�ĶԽ��߳���ǡ����ȣ����߿��������ǿ�ų��У��ų��ĴŸ�Ӧǿ�ȷ���ֱ���߿�����ƽ�����������MN�뵼�߿�Ӵ����ã��ҵ��߿�Խ���BD��ֱƽ��MN����������B�����������˶���AC�Ĺ����У�������| A�� | ABCD���ĵĵ繦�����ܵĵ繦��֮�Ȳ��ϼ�С��50% | |
| B�� | MN�������Ĺ����ȼ�С������ | |
| C�� | MN����������� | |
| D�� | ���������D��Ͽ�����MN�е������� |
���� �ɵ�����˶��ٶȵõ�����ʱ�䵼�����λ�ã������õ�����������·�ij��ȣ������õ��綯�ƣ�Ȼ����ݵ�·��õ����������õ������������õ��������ƽ��״̬�õ�������������������Ĺ��ʣ�
��� �⣺A����������B�����������˶���AC�Ĺ��̣����ٶ�Ϊv����ô����ʱ��tʱ��������Ͻ����·�ĵ綯��Ϊ��E=2Bv2t��
�赼���߳�Ϊa����λ���ȵĵ���ΪR0����MN�����·�ĵ���Ϊ��r=2R0vt��������ڵ�������ĵ���Ϊ��${R}_{1}=2\sqrt{2}{R}_{0}vt$���Ҳ����Ϊ��${R}_{2}=4a{R}_{0}-2\sqrt{2}{R}_{0}vt$��
���ԣ����·����Ϊ��$R=\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}=\frac{\sqrt{2}vt��2a{R}_{0}-\sqrt{2}{R}_{0}vt��}{a}$=$��2\sqrt{2}-\frac{2vt}{a}��{R}_{0}vt$��
�����ڵ�·���������·�ܵ�����С��ȣ�����ABCD���ĵĵ繦�����ܵĵ繦��֮��Ϊ$\frac{R}{R+r}=\frac{2\sqrt{2}-\frac{2vt}{a}}{2+2\sqrt{2}-\frac{2vt}{a}}$=$1-\frac{1}{1+\sqrt{2}-\frac{vt}{a}}$����Ϊ��������B�����������˶���AC�Ĺ����У���$0��t��\frac{a}{\sqrt{2}v}$�����ԣ���t����ABCD���ĵĵ繦�����ܵĵ繦��֮�Ȳ��ϼ�С����С��$1-\frac{1}{1+\sqrt{2}-\frac{v��\frac{a}{\sqrt{2}v}}{a}}=1-\frac{1}{1+\sqrt{2}-\frac{\sqrt{2}}{2}}$=$1-2��1-\frac{\sqrt{2}}{2}��=\sqrt{2}-1$����A����
C����A��֪MN�е���$I=\frac{E}{r+R}=\frac{2B{v}^{2}t}{��2+2\sqrt{2}-\frac{2vt}{a}��{R}_{0}vt}$=$\frac{Bv}{��1+\sqrt{2}-\frac{vt}{a}��{R}_{0}}$������t����I��������C��ȷ��
B��MN�������Ĺ���P=Fv=2BIv2t=$\frac{2{B}^{2}{v}^{3}t}{��1+\sqrt{2}-\frac{vt}{a}��{R}_{0}}$=$\frac{2{B}^{2}{v}^{3}}{��\frac{1+\sqrt{2}}{t}-\frac{v}{a}��{R}_{0}}$����Ϊ��������B�����������˶���AC�Ĺ����У���$0��t��\frac{a}{\sqrt{2}v}$������t����P����B����
D�����������D��Ͽ�����綯�Ʋ��䣬���費�䣬���������ԣ�MN�е�����С����D����
��ѡ��C��
���� �պϵ�·�и�Ÿ������⣬һ����ݱպϵ�·�˶���õ綯�ƣ�Ȼ���ɵ�·ԭ����õ�����������ð��������繦�ʡ������������⣮


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
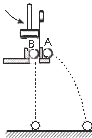 ��ͼ��ʾ����С��������Խ���Ƭ��A��ˮƽ�ɳ���ͬʱB���ͷ��������£����ƿ��������������ж���ȷ���ǣ�������
��ͼ��ʾ����С��������Խ���Ƭ��A��ˮƽ�ɳ���ͬʱB���ͷ��������£����ƿ��������������ж���ȷ���ǣ�������| A�� | A������� | B�� | B������� | ||
| C�� | ����ͬʱ��� | D�� | �������ʱ���ٶ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | 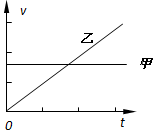 | B�� | 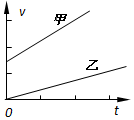 | ||
| C�� | 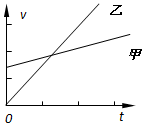 | D�� | 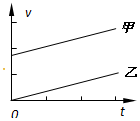 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ijʵ��С�������˸����ɵ���װ�ã����ʵ��ɺ���������С������ڼ����⻬�Ľ������У���������ˮƽ�̶��ڸߴ�����ʼʱѹ�����ɲ�������ʹ�����뵯�����˸պýӴ���Ȼ�����Ե��ɵ�������������ӽ����ܵ����˵����ȥ��ʵ��С�����������ʵ������Ͳ��裮��g=9.8m/s2��
ijʵ��С�������˸����ɵ���װ�ã����ʵ��ɺ���������С������ڼ����⻬�Ľ������У���������ˮƽ�̶��ڸߴ�����ʼʱѹ�����ɲ�������ʹ�����뵯�����˸պýӴ���Ȼ�����Ե��ɵ�������������ӽ����ܵ����˵����ȥ��ʵ��С�����������ʵ������Ͳ��裮��g=9.8m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
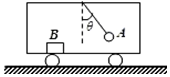 ��ͼ��ʾ��С���˶��Ĺ����У�������Ϊm�����ҵ�С��A�ͳ�ˮƽ�װ��ϵ����B����Գ��ᾲֹ������С��A����������ֱ�н�Ϊ�ȣ������B�ܵ���Ħ������С���˶���������ж�����ȷ���ǣ�������
��ͼ��ʾ��С���˶��Ĺ����У�������Ϊm�����ҵ�С��A�ͳ�ˮƽ�װ��ϵ����B����Գ��ᾲֹ������С��A����������ֱ�н�Ϊ�ȣ������B�ܵ���Ħ������С���˶���������ж�����ȷ���ǣ�������| A�� | ���B����Ħ�������ã�С��ֻ�������˶� | |
| B�� | ���B��Ħ�������ã���СΪmgtan�ȣ���������С�����������˶� | |
| C�� | ���B��Ħ�������ã���СΪmgtan�ȣ���������С��һ�������˶� | |
| D�� | B�ܵ���Ħ����������жϣ�С���˶�������ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
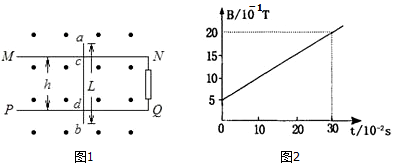
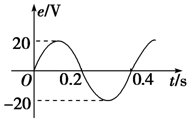 С�ͽ���������У����ν�����Ȧ����ǿ�ų�������ת���������ĸ�Ӧ�綯����ʱ������Һ�����ϵ����ͼ��ʾ������Ȧ��һ��R=9���ĵ��蹹�ɱպϵ�·����Ȧ�����ĵ���r=1��������˵����ȷ���ǣ�������
С�ͽ���������У����ν�����Ȧ����ǿ�ų�������ת���������ĸ�Ӧ�綯����ʱ������Һ�����ϵ����ͼ��ʾ������Ȧ��һ��R=9���ĵ��蹹�ɱպϵ�·����Ȧ�����ĵ���r=1��������˵����ȷ���ǣ�������| A�� | �������������Ϊ0.2 s | B�� | ���������Ƶ��Ϊ2.5 Hz | ||
| C�� | �������������Ϊ2 A | D�� | ���������ĵ繦��Ϊ18 W |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
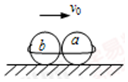 ��ͼ�������ֱ�Ϊm1=1.0kg�ĵ���С��a��m2=2.0kg�ĵ���С��b�����������������İ���������һ��ʹ���Ƿ���С���α䣮��ϵͳ���ٶ�v0=0.10m/s�ع⻬ˮƽ������������ֱ���˶���ijʱ������ͻȻ�Զ��Ͽ����Ͽ�����������ԭֱ���˶�������ʱ��t=5.0s����������s=4.5m��������˵����ȷ���ǣ�������
��ͼ�������ֱ�Ϊm1=1.0kg�ĵ���С��a��m2=2.0kg�ĵ���С��b�����������������İ���������һ��ʹ���Ƿ���С���α䣮��ϵͳ���ٶ�v0=0.10m/s�ع⻬ˮƽ������������ֱ���˶���ijʱ������ͻȻ�Զ��Ͽ����Ͽ�����������ԭֱ���˶�������ʱ��t=5.0s����������s=4.5m��������˵����ȷ���ǣ�������| A�� | �շ���ʱ��a����ٶȴ�СΪ1.1m/s | |
| B�� | �շ���ʱ��b����ٶȴ�СΪ0.2m/s | |
| C�� | �շ���ʱ��a��b������ٶȷ�����ͬ | |
| D�� | ����ֿ��������ͷŵĵ�������Ϊ0.1J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com