
 如图甲所示,在光滑绝缘水平桌面内建立xOy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°.在第 III象限垂直于桌面放置两块相互平行的平板c1、c2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板c1与x轴重合,在其左端紧贴桌面有一小孔M,小孔M离坐标原点O的距离为L=0.72m.在第Ⅳ象限垂直于x轴放置一块平行y轴且沿y轴负向足够长的竖直平板c3,平板c3在x轴上垂足为Q,垂足Q与原点O相距d2=0.18m.现将一带负电的小球从桌面上的P点以初速度v0=42m/s垂直于电场方向射出,刚好垂直于x轴穿过c1板上的M孔,进人磁场区域.已知小球可视为质点,小球的比荷qm=20C/kg,P点与小孔M在垂直于电场方向上的距离为s=210m,不考虑空气阻力.求:
如图甲所示,在光滑绝缘水平桌面内建立xOy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°.在第 III象限垂直于桌面放置两块相互平行的平板c1、c2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板c1与x轴重合,在其左端紧贴桌面有一小孔M,小孔M离坐标原点O的距离为L=0.72m.在第Ⅳ象限垂直于x轴放置一块平行y轴且沿y轴负向足够长的竖直平板c3,平板c3在x轴上垂足为Q,垂足Q与原点O相距d2=0.18m.现将一带负电的小球从桌面上的P点以初速度v0=42m/s垂直于电场方向射出,刚好垂直于x轴穿过c1板上的M孔,进人磁场区域.已知小球可视为质点,小球的比荷qm=20C/kg,P点与小孔M在垂直于电场方向上的距离为s=210m,不考虑空气阻力.求:分析 本题是一个球在光滑绝缘的桌面上先在电场中做类平抛运动,后进入磁场做匀速圆周运动的特例
(1).M点的速度就是粒子做类平抛运动的末速度,已知平抛的初速度和末速度的方向,由速度的分解很方便的求出.
(2).根据类平抛运动的位移公式和几何关系可求得粒子在电场中的加速度,从而求出场强的大小.
(3).要使小球打在板上,先要考虑B越大,半径越小,越容易从OQ之间穿出,则要考虑刚好打在Q点的情况;另外若B越小,半径越大,则有可能打到下板上,所以当B最小时,轨迹与下板相切.
解答 解:(1)小球在第II象限做类平抛运动,由速度的分解可得:
$v=\frac{{v}_{0}}{sinθ}=8m/s$
(2)垂直电场方向的位移:s=v0t ①
平行于电场方向的速度关系有:at=v0tanθ ②
由牛顿第二定律:qE=ma ③
联立上述式解得:$E=8\sqrt{2}V/m$
(3)小球进入两板间做匀速圆周运动,轨迹如图: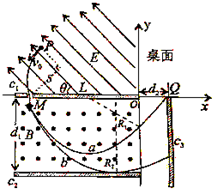
由洛仑兹力提供向心力有:
$qvB=\frac{m{v}^{2}}{R}$
解得:$B=\frac{mv}{qR}$
小球刚好能打到Q点时,磁感应强度最大设为B1.此时小球的轨迹半径为R1,由两个直角三角形相似的几何关系有:
$\frac{{R}_{1}}{L+{d}_{2}-{R}_{1}}=\frac{L-{R}_{1}}{{R}_{1}}$
解得:
R1=0.4m
B1=1T
小球刚好不与c2板相碰时,磁感应强度最大设为B2.此时小球的轨迹半径为R2,由几何关系有:
R1=d1
解得:${B}_{2}=\frac{2}{3}T$
故:磁感应强度的取值范围:
$\frac{2}{3}T≤B≤1T$
答:(1)M点速度大小8m/s.
(2)匀强电场的场强大小$8\sqrt{2}V/m$.
(3)要使带电小球无碰撞地穿出磁场并打到平板c3上,磁感应强度的取值范围为$\frac{2}{3}T≤B≤1T$.
点评 第①②小题还属于类平抛与圆周运动的综合,结合牛顿运动定律不难解出,本题的难点在于第③问B的最大值,刚好打在Q点时,这有两个相似的直角三角形,根据相似关系求出最小的半径(对应B的最大值).


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中物理 来源: 题型:多选题
| A. | 速度变化越快,加速度一定越大 | |
| B. | 速度变化越大,加速度一定越大 | |
| C. | 速度变化但所用的时间越短,加速度一定越大 | |
| D. | 单位时间内速度变化越大,加速度一定越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
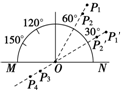 如图所示,一半圆形玻璃砖外面插上P1、P2、P3、P4四枚大头针时,P3、P4恰可挡住P1、P2所成的像,则该玻璃砖的折射率n=1.73.有一同学把大头针插在P1′和P2′位置时,沿着P4、P3 的方向看不到大头针的像,其原因是经过P1′P2′的光线在MN处发生全反射.
如图所示,一半圆形玻璃砖外面插上P1、P2、P3、P4四枚大头针时,P3、P4恰可挡住P1、P2所成的像,则该玻璃砖的折射率n=1.73.有一同学把大头针插在P1′和P2′位置时,沿着P4、P3 的方向看不到大头针的像,其原因是经过P1′P2′的光线在MN处发生全反射.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
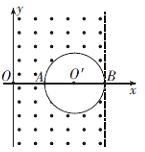 如图所示,在xOy平面内,有一个圆形区域,其直径AB与x轴重合,圆心O′的坐标为(2a,O),其半径为a,该区域内无磁场. 在y轴和直线x=3a之间的其他区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电的粒子从y轴上某点射入磁场.不计粒子重力.
如图所示,在xOy平面内,有一个圆形区域,其直径AB与x轴重合,圆心O′的坐标为(2a,O),其半径为a,该区域内无磁场. 在y轴和直线x=3a之间的其他区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电的粒子从y轴上某点射入磁场.不计粒子重力.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
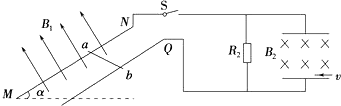
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:填空题
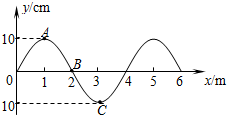 一列沿x正方向传播的横波,在t=0时刻的波形如图所示,则A点的振幅为10 cm,波长为4 m,此时质点B的速度方向为沿y轴正方向 (填“沿y轴正方向”或“沿y轴负方向”).若波速为10m/s,则从0至5s内质点C经过的路程为5m.
一列沿x正方向传播的横波,在t=0时刻的波形如图所示,则A点的振幅为10 cm,波长为4 m,此时质点B的速度方向为沿y轴正方向 (填“沿y轴正方向”或“沿y轴负方向”).若波速为10m/s,则从0至5s内质点C经过的路程为5m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com