
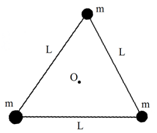
 宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三颗星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是.
宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三颗星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是.| A. | 每颗星做圆周运动的角速度为$\sqrt{\frac{3Gm}{{L}^{3}}}$ | |
| B. | 每颗星做圆周运动的加速度与三星的质量有关 | |
| C. | 若距离L和每颗星的质量m都变为原来的2倍,则周期变为原来的2倍 | |
| D. | 若距离L和每颗星的质量m都变为原来的2倍,则线速度变为原来的4倍 |
分析 先写出任意两个星星之间的万有引力,求每一颗星星受到的合力,该合力提供它们的向心力.
然后用R表达出它们的轨道半径,最后写出用周期和线速度表达的向心力的公式,整理即可的出结果.
解答 解:A、任意两个星星之间的万有引力F=$\frac{Gmm}{{L}^{2}}$每一颗星星受到的合力,F1=$\sqrt{3}$F,由几何关系知:它们的轨道半径r=$\frac{\sqrt{3}}{3}$L…①
合力提供它们的向心力:$\frac{\sqrt{3}Gmm}{{R}^{2}}$=m$\frac{{v}^{2}}{r}$…②
联立①②,解得:v=$\sqrt{\frac{GM}{L}}$,故A错误.
B、任意两个星星之间的万有引力F=$\frac{Gmm}{{L}^{2}}$每一颗星星受到的合力就是其向心力,F1=$\sqrt{3}$F,由牛顿第二定律可知可知,a=$\frac{F}{m}$=$\frac{\sqrt{3}Gm}{{R}^{2}}$向心加速度与质量有关,故B正确;
C、由$\frac{\sqrt{3}Gmm}{{R}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}r$解得:T=$\frac{2}{3}π\sqrt{\frac{3{L}^{2}}{Gm}}$,若距离L和每颗星的质量m都变为原来的2倍,则周期变为原来的2倍;故C正确;
D、由A可知v=$\sqrt{\frac{GM}{L}}$,则可知,L和每颗星的质量m都变为原来的2倍,则线速度不变,故D错误.
故选:BC.
点评 解决该题首先要理解模型所提供的情景,然后能够列出合力提供向心力的公式,根据公式进行分析才能明确各物理量发生变化时周期和线速度等的变化情况.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
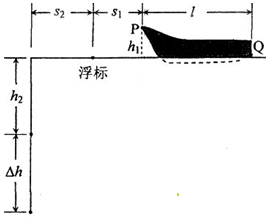 一赛艇停在平静的水面上,赛艇前端有一标记P离水面的高度为h1=0.6m,尾部下端Q略高于水面;赛艇正前方离赛艇前端s1=0.8m处有一浮标,示意如图.一潜水员在浮标前方s2=3.0m 处下潜到深度为h2=4.0m 时,看到标记刚好被浮标挡住,此处看不到船尾端 Q;继续下△h=4.0m,恰好能看见Q.求:
一赛艇停在平静的水面上,赛艇前端有一标记P离水面的高度为h1=0.6m,尾部下端Q略高于水面;赛艇正前方离赛艇前端s1=0.8m处有一浮标,示意如图.一潜水员在浮标前方s2=3.0m 处下潜到深度为h2=4.0m 时,看到标记刚好被浮标挡住,此处看不到船尾端 Q;继续下△h=4.0m,恰好能看见Q.求:查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 位移、时间、速度、温度 | B. | 速度、速度变化量、加速度、位移 | ||
| C. | 速度、速率、加速度、力 | D. | 路程、时间、速度、加速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 物体的速度变化量越大,加速度越大 | |
| B. | 加速度的方向与速度变化的方向相同 | |
| C. | 加速度减小的运动一定是减速运动 | |
| D. | 若初速度方向与加速度方向一致,当加速度减小到零时,速度达到最大值 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止开始做匀加速直线运动,下列结论正确的是( )
如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止开始做匀加速直线运动,下列结论正确的是( )| A. | $\frac{{x}_{AB}}{{{t}_{AB}}^{2}}$=$\frac{{x}_{AC}}{{{t}_{AC}}^{2}}$=$\frac{{x}_{AD}}{{{t}_{AD}}^{2}}$=$\frac{{x}_{AE}}{{{t}_{AE}}^{2}}$ | |
| B. | $\frac{{x}_{AB}}{{t}_{AB}}$=$\frac{{x}_{BC}}{{t}_{BC}}$=$\frac{{x}_{CD}}{{t}_{CD}}$=$\frac{{x}_{DE}}{{t}_{DE}}$ | |
| C. | tAB:tBC:tCD:tDE=1:($\sqrt{2}-1$):($\sqrt{3}-\sqrt{2}$):(2-$\sqrt{3}$) | |
| D. | vE=$\sqrt{2}$vB |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,A点离M板4mm,A、B相距4mm,电场强度大小为1×104V/m,A点电势为-60V,B点电势为-40V.若将q=-10-6C的点电荷从A移到B,电场力做了2×10-5J的正功.
如图所示,A点离M板4mm,A、B相距4mm,电场强度大小为1×104V/m,A点电势为-60V,B点电势为-40V.若将q=-10-6C的点电荷从A移到B,电场力做了2×10-5J的正功.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com