
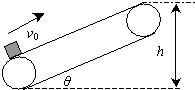
 如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持v0=5m/s的速率运行方向斜向上.现把一质量m=10kg的工件(可看为质点)轻轻放在皮带的底端,工件被传送到皮带的顶端h=0.625m的高处,取g=10m/s2.已知动摩擦因数为μ=
如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持v0=5m/s的速率运行方向斜向上.现把一质量m=10kg的工件(可看为质点)轻轻放在皮带的底端,工件被传送到皮带的顶端h=0.625m的高处,取g=10m/s2.已知动摩擦因数为μ= .
.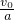 =2s
=2s at2=5m
at2=5m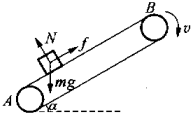
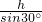 =1.25m.
=1.25m.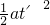


科目:高中物理 来源: 题型:
 (2010?越秀区三模)如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量m=10kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.求:
(2010?越秀区三模)如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量m=10kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,绷紧的传送带与水平而的夹角θ=30°,皮带在电动机的带动下,始终保持v=2m/s的速率运行.现把m=10kg的工件(可看作质点)轻轻放在皮带的底端,经时间1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.求工件与皮带间的动摩擦因数.
如图所示,绷紧的传送带与水平而的夹角θ=30°,皮带在电动机的带动下,始终保持v=2m/s的速率运行.现把m=10kg的工件(可看作质点)轻轻放在皮带的底端,经时间1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.求工件与皮带间的动摩擦因数.查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持v0=2.5m/s的速率运行.将一质量m=1kg的工件(可看为质点)轻轻放在皮带的底端A点,工件能被传送到顶端B点,h=2.5m.已知工件与皮带间的动摩擦因数μ=
如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持v0=2.5m/s的速率运行.将一质量m=1kg的工件(可看为质点)轻轻放在皮带的底端A点,工件能被传送到顶端B点,h=2.5m.已知工件与皮带间的动摩擦因数μ=
| ||
| 2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量为m=1kg的工件(可看为质点)轻轻放在传送带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,并取得了与传送带相同的速度,取g=10m/s2.求:
如图所示,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量为m=1kg的工件(可看为质点)轻轻放在传送带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,并取得了与传送带相同的速度,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,绷紧的传送带与水平面的夹角α=30°,皮带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量m=10kg的工件(可视为质点)轻轻放在皮带的底端,工件将被传送到h=2m的高处.设工件与皮带间的动摩擦因数μ=△s=v0t1-
如图所示,绷紧的传送带与水平面的夹角α=30°,皮带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量m=10kg的工件(可视为质点)轻轻放在皮带的底端,工件将被传送到h=2m的高处.设工件与皮带间的动摩擦因数μ=△s=v0t1-| v0 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com