
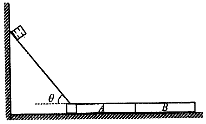
 ��ͼ��ʾ����һ�鳤L1=2.5m��ľ�壨ľ���¶���һ�ϱ���⻬��������߶���ľ��A��B��ͬ����ǽ�͵�������б�棬б����ˮƽ�������Ǧȿ���0��60�����ں�̶���������m1=5kg��С����б�涥�˾�ֹ�ͷţ�Ϊ����С�������淢��ײ�����ڵ����Ͻ���������Ĺ⻬�����������ŷ�������ȫ��ͬ��ľ��A��B�����Ⱦ�Ϊl=2m��������Ϊm2=10kg������С�����ת�Ǵ��͵����˶���������ʧ���������б���Ķ�Ħ��������=0.125�������ľ���Ķ�Ħ��������1=0.4��ľ��������Ķ�Ħ��������2=0.1�����Ħ�������ڻ���Ħ�������������ٶ�g=10m/s2��
��ͼ��ʾ����һ�鳤L1=2.5m��ľ�壨ľ���¶���һ�ϱ���⻬��������߶���ľ��A��B��ͬ����ǽ�͵�������б�棬б����ˮƽ�������Ǧȿ���0��60�����ں�̶���������m1=5kg��С����б�涥�˾�ֹ�ͷţ�Ϊ����С�������淢��ײ�����ڵ����Ͻ���������Ĺ⻬�����������ŷ�������ȫ��ͬ��ľ��A��B�����Ⱦ�Ϊl=2m��������Ϊm2=10kg������С�����ת�Ǵ��͵����˶���������ʧ���������б���Ķ�Ħ��������=0.125�������ľ���Ķ�Ħ��������1=0.4��ľ��������Ķ�Ħ��������2=0.1�����Ħ�������ڻ���Ħ�������������ٶ�g=10m/s2������ ��1��������ƽ����⣻
��2���������б�����˶�Ӧ�ö��ܶ�����û���A���ٶȣ�Ȼ��������������õ�����A���˶������ɶ��ܶ������С��鵽��ľ��Aĩ�˵��ٶȣ�
��3��������黬��B������B���˶��������ȱ����˶��������������λ�ƣ����ɵõ���������״̬��
��� �⣺��1����С����Ħ����Ϊ���Ħ������С�����б��������ƽ��ʱ�ܴ�б�濪ʼ�»������У�m1gsin��=��m1gcos�ȣ����ԣ�$tan��=\frac{1}{8}$��$��=arctan\frac{1}{8}$��
��2����С�����б���ϵ��˶�Ӧ�ö��ܶ����ɵã�${m}_{1}g{L}_{1}sin37��-��{m}_{1}g{L}_{1}cos37��=\frac{1}{2}{m}_{1}{v}^{2}$�����ԣ���黬��A���ٶ�$v=\sqrt{2g{L}_{1}��sin37��-��cos37�㣩}=5m/s$��
�����A�ϻ�����AB��Ϊһ�����壬һ�������˶�����AB���ٶ�С������ٶ�ʱ����������ٶ�$a=\frac{{��}_{1}{m}_{1}g}{{m}_{1}}={��}_{1}g=4m/{s}^{2}$���ȼ����˶���
��Ϊ��2��m1+2m2��g����1m1g�����ԣ�AB���־�ֹ��
��ô�������A���˶�Ӧ�ö��ܶ����ɵã�$-{��}_{1}{m}_{1}gl=\frac{1}{2}{m}_{1}{{v}_{1}}^{2}-\frac{1}{2}{m}_{1}{v}^{2}$�����ԣ�С��鵽��ľ��Aĩ�˵��ٶ�${v}_{1}=\sqrt{{v}^{2}-2{��}_{1}gl}=3m/s$��
��3����B���ٶ�С������ٶ�ʱ�������B�������ٶ�$a=\frac{{��}_{1}{m}_{1}g}{{m}_{1}}={��}_{1}g=4m/{s}^{2}$���ȼ����˶���B�����ٶ�$a��=\frac{{��}_{1}{m}_{1}g-{��}_{2}��{m}_{1}+{m}_{2}��g}{{m}_{2}}=0.5m/{s}^{2}$�ļ����˶���
�辭��ʱ��t��ﵽ��ͬ�ٶȣ���ô��v1-at=a��t�����ԣ�$t=\frac{2}{3}s$��
��ô���ߵ����λ��$s={v}_{1}t-\frac{1}{2}a{t}^{2}-\frac{1}{2}a��{t}^{2}=1m��l$��
�ﵽ��ͬ�ٶȺ�����B������Ծ�ֹ���ʻ��ﲻ���ľ��B���Ҷ˻��䣬�һ�������ͣ��B���ϵ��е㣻
�𣺣�1�����Ƚ�����$arctan\frac{1}{8}$ʱ��С����ܴ�б�濪ʼ�»���
��2����������37��ʱ��С��鵽��ľ��Aĩ�˵��ٶ�Ϊ3m/s��
��3���ڣ�2���ʵ�����£����ﲻ���ľ��B���Ҷ˻��䣻��������ͣ��B���ϵ��е㣮
���� ������ѧ����һ���ȶ��������������������ú��������˶��������������Ȼ�����ţ�ٶ��ɡ����ܶ��������ι�ϵ��⣮


 �ŵ������ϵ�д�
�ŵ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ǵ����� | B�� | ���ǵ��ܶ� | ||
| C�� | ���ǵĽ��ٶ� | D�� | ���ǵı����������ٶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
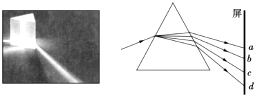
| A�� | ����d�����Ϲ� | |
| B�� | ����d���Ĺ����⾵�д����ٶ���� | |
| C�� | ����a�����Ϲ� | |
| D�� | ����a���Ĺ����⾵�д����ٶ���С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
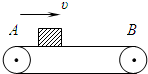 ��ͼ��ʾ��ˮƽ���ʹ���v=2m/s���ٶ������˶���A��B�������s=11m��һ����m=1kg����飨����Ϊ�ʵ㣩��A���ɾ�ֹ��ʼ�˶�����֪����봫�ʹ���Ķ�Ħ��������=0.2���������ٶ�g=10m/s2��
��ͼ��ʾ��ˮƽ���ʹ���v=2m/s���ٶ������˶���A��B�������s=11m��һ����m=1kg����飨����Ϊ�ʵ㣩��A���ɾ�ֹ��ʼ�˶�����֪����봫�ʹ���Ķ�Ħ��������=0.2���������ٶ�g=10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ��AB�����Ϊ��=30��Ĵֲ�ֱ�����BCD�ǹ⻬��Բ�������ABǡ����B����Բ�����У�Բ���İ뾶ΪR��һ������Ϊm�����壨���Կ����ʵ㣩��ֱ����ϵ�P���ɾ�ֹ�ͷţ������������������������˶�����֪P����Բ����Բ��O�ȸߣ������������˶���������������AB�����ͨ����·��Ϊs����
��ͼ��ʾ��AB�����Ϊ��=30��Ĵֲ�ֱ�����BCD�ǹ⻬��Բ�������ABǡ����B����Բ�����У�Բ���İ뾶ΪR��һ������Ϊm�����壨���Կ����ʵ㣩��ֱ����ϵ�P���ɾ�ֹ�ͷţ������������������������˶�����֪P����Բ����Բ��O�ȸߣ������������˶���������������AB�����ͨ����·��Ϊs�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
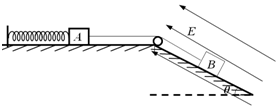 ��ͼ��ʾ������A�ʹ����������B�ÿ�������ֵľ�Ե�������ӣ�A��B�������ֱ���m��2m������ϵ��Ϊk�����ʵ���һ�˹̶���ˮƽ���ϣ���һ��������A���������Ϊ�ȵ�б�洦����б�����ϵ���ǿ�糡�У�����ϵͳ����һ��Ħ������ʼʱ������B��һ��б�����ϵ�����F=3mgsin�ȵ������±��־�ֹ������ǡ����ֱ��Ȼ��ȥ����F��ֱ������B�������ٶȣ��ҵ���δ���������ȣ����ڴ˹����У�������
��ͼ��ʾ������A�ʹ����������B�ÿ�������ֵľ�Ե�������ӣ�A��B�������ֱ���m��2m������ϵ��Ϊk�����ʵ���һ�˹̶���ˮƽ���ϣ���һ��������A���������Ϊ�ȵ�б�洦����б�����ϵ���ǿ�糡�У�����ϵͳ����һ��Ħ������ʼʱ������B��һ��б�����ϵ�����F=3mgsin�ȵ������±��־�ֹ������ǡ����ֱ��Ȼ��ȥ����F��ֱ������B�������ٶȣ��ҵ���δ���������ȣ����ڴ˹����У�������| A�� | ��ȥ����F��˲�䣬����A�ļ��ٶ�Ϊgsin�� | |
| B�� | ��ȥ����F��˲�䣬����B�ļ��ٶ�Ϊ$\frac{3gsin��}{2}$ | |
| C�� | A��B�������ٶ�ʱ�������쳤��Ϊ $\frac{3mgsin��}{k}$ | |
| D�� | ����A�͵�����ɵ�ϵͳ��е���غ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{A-4}{A+4}$ | B�� | $\frac{{{{��A+4��}^2}}}{{{{��A-4��}^2}}}$ | C�� | $\frac{4A}{{{{��A+4��}^2}}}$ | D�� | $\frac{A+4}{A-4}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ԭ�����չ��ӣ����ӵĶ��ܼ�С��ԭ�ӵĵ���������ԭ�ӵ��������� | |
| B�� | ԭ�����չ��ӣ����ӵĶ�������ԭ�ӵĵ����ܼ�С��ԭ�ӵ��������� | |
| C�� | ԭ�ӷų����ӣ����ӵĶ�������ԭ�ӵĵ����ܼ�С��ԭ�ӵ�������С | |
| D�� | ԭ�ӷų����ӣ����ӵĶ��ܼ�С��ԭ�ӵĵ���������ԭ�ӵ�������С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ������ˮƽת̨�ϵ�С����A��B��C����ת̨һ���Խ��ٶȦ�����ת����ABC�������ֱ�Ϊ3m��2m��2m��A��B��B��ת̨��C��ת̨��Ķ�Ħ��������Ϊ�̣�BC��ת̨���ĵľ���ֱ�Ϊr��1.5r�������Ħ�������ڻ���Ħ����������˵����ȷ���ǣ�������
��ͼ��ʾ������ˮƽת̨�ϵ�С����A��B��C����ת̨һ���Խ��ٶȦ�����ת����ABC�������ֱ�Ϊ3m��2m��2m��A��B��B��ת̨��C��ת̨��Ķ�Ħ��������Ϊ�̣�BC��ת̨���ĵľ���ֱ�Ϊr��1.5r�������Ħ�������ڻ���Ħ����������˵����ȷ���ǣ�������| A�� | ��C��ת̨���Ħ������С����A��B���Ħ������С | |
| B�� | ��B��A��Ħ������Сһ��Ϊ3��mg | |
| C�� | ����ת̨���ٶȦ�����A������������ˮƽת̨ת̨�� | |
| D�� | ���ٶ�һ�����㣺�ء�$\sqrt{\frac{2��g}{3r}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com