
 如图所示.一束截面为圆形,半径R=0.2m的平行光垂直射向一玻璃半球的平面.经折射后在屏幕S上形成一个圆形亮区.已知玻璃半球的半径为R=0.2m.屏幕S至球心的距离为D=$\frac{\sqrt{2}}{2}$m.不考虑光的干涉和衍射,试问:
如图所示.一束截面为圆形,半径R=0.2m的平行光垂直射向一玻璃半球的平面.经折射后在屏幕S上形成一个圆形亮区.已知玻璃半球的半径为R=0.2m.屏幕S至球心的距离为D=$\frac{\sqrt{2}}{2}$m.不考虑光的干涉和衍射,试问:分析 (i)当光线从空气垂直射入半圆玻璃砖,光线不发生改变,当入射角小于临界角时,光线才能再从玻璃砖射出,所以平行白光中的折射率不同,导致临界角不同,因此偏折程度不同,从而确定圆形亮区的最外侧的颜色.
(ii)光线沿直线从O点穿过玻璃,方向不变.从A点射出玻璃砖的光线方向向左偏折,射到屏幕S上圆形亮区,作出光路图,由光的折射定律结合数学几何知识求出圆形亮区的半径,从而求得屏幕上圆形亮区的面积.
解答 解:(i)复色光与半球形玻璃面的下表面相垂直,方向不变,但是在上面的圆弧面会发生偏折,紫光的折射率最大,所以紫光偏折的最多,且屏上相应的光点与入射光线在玻璃半球的对称轴两侧,因此最外侧是紫色.
(ii)如图所示.紫光刚要发生全反射时的临界光线射在屏幕S上的点D到亮区中心E的距离r就是所求最大半径.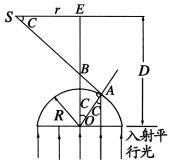
设紫光临界角为C.由全反射的知识:sinC=$\frac{1}{n}$
所以cosC=$\sqrt{1-si{n}^{2}C}$=$\frac{\sqrt{{n}^{2}-1}}{n}$
tanC=$\frac{sinC}{cosC}$=$\frac{1}{\sqrt{{n}^{2}-1}}$
根据几何关系得 OB=$\frac{R}{cosC}$=$\frac{nR}{\sqrt{{n}^{2}-1}}$
屏幕上圆形亮区的半径 r=$\frac{D-OB}{tanC}$=D$\sqrt{{n}^{2}-1}$-nR
代入数据解得 r=$\frac{5-\sqrt{3}}{5}$m
所以屏幕上圆形亮区的面积 S=πr2=$\frac{28-10\sqrt{3}}{25}$π(m2)
答:
(i)最外侧是紫色.
(ii)屏幕上圆形亮区的面积是$\frac{28-10\sqrt{3}}{25}$π(m2).
点评 本题考查光的折射.关键是作出光路图,根据几何知识求出入射角与折射角,知道折射率和临界角的关系,了解各种色光的波长和折射率的关系.


科目:高中物理 来源: 题型:计算题
 如图所示,绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E,磁场方向垂直纸面向外,磁感应强度大小为B.一质量为m,电荷量为q的带正电的小滑块从A点由静止开始沿MN下滑,到达C点时离开MN做曲线运动.A、C两点间距离为h,重力加速度为g.
如图所示,绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E,磁场方向垂直纸面向外,磁感应强度大小为B.一质量为m,电荷量为q的带正电的小滑块从A点由静止开始沿MN下滑,到达C点时离开MN做曲线运动.A、C两点间距离为h,重力加速度为g.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 (1)质量为5kg的物体从高16m的地方由静止开始下落,着地时速度为16m/s,试求物体在下落过程中所受的平均阻力是多大?(g=10m/s2)
(1)质量为5kg的物体从高16m的地方由静止开始下落,着地时速度为16m/s,试求物体在下落过程中所受的平均阻力是多大?(g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一质量为50kg的人站在上升的升降机的地板上,他看到弹簧测力计示数为40N,而挂在弹簧测力计下的物体A的质量为5kg.如图所示,g取10m/s2,求:
一质量为50kg的人站在上升的升降机的地板上,他看到弹簧测力计示数为40N,而挂在弹簧测力计下的物体A的质量为5kg.如图所示,g取10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,真空中有一平行玻璃砖,一束单色光从光源P发出与界面成θ=30°角从ab面中点射入,测得折射角α=45°,在玻璃砖的右侧面ad射出,假设,光从光源P到ab面上的O点的传播时间和它在玻璃砖中传播的时间相等,已知光在真空中的传播速度c=3.0×108m/s,ab边长为$\sqrt{3}$×10cm,求:
如图所示,真空中有一平行玻璃砖,一束单色光从光源P发出与界面成θ=30°角从ab面中点射入,测得折射角α=45°,在玻璃砖的右侧面ad射出,假设,光从光源P到ab面上的O点的传播时间和它在玻璃砖中传播的时间相等,已知光在真空中的传播速度c=3.0×108m/s,ab边长为$\sqrt{3}$×10cm,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示为一滑梯的示意图,滑梯的长度AB为x=8m,倾角θ=37°.BC段为与滑梯平滑连接的水平地面.一个小孩从滑梯顶端由静止开始滑下,离开B点后在地面上滑行了x′=6.4m后停下.小孩与滑梯间的动摩擦因数为μ0=0.25.不计空气阻力.取g=10m/s2.已知sin37°=0.6,cos37°=0.8.求:
如图所示为一滑梯的示意图,滑梯的长度AB为x=8m,倾角θ=37°.BC段为与滑梯平滑连接的水平地面.一个小孩从滑梯顶端由静止开始滑下,离开B点后在地面上滑行了x′=6.4m后停下.小孩与滑梯间的动摩擦因数为μ0=0.25.不计空气阻力.取g=10m/s2.已知sin37°=0.6,cos37°=0.8.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 为了形象的描述磁场,引入了磁感线 | |
| B. | 磁感应强度用物理符号E表示 | |
| C. | 小磁针静止时N极所指的方向就是该点磁感应强度的方向 | |
| D. | 在磁感线越密的地方说明该点磁感应强度越小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com