Question

用一个半球形容器和三个小球可以进行有趣的碰撞实验.三个质量分别为m₁、m₂、m₃的小球1,2,3，半径相同且可视为质点,自左向右依次静置于容器底部的同一直线上彼此相互接触.若将质量为m₁的小球移至左侧离容器底高h处无初速释放,如图所示,则三个小球间将发生一系列碰撞.已知容器内侧面光滑,半径为R,各小球间的碰撞时间极短且碰撞时无机械能损失.

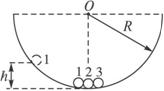
(1)若三个小球的质量均为m且令h远小于R,则小球在碰撞时将交换速度,且三个小球组成的系统的运动是周期性的,求此系统的运动周期T.

(2)若三个小球的质量不同且成一定比例,当h为某一定值h₀时,球1与球2碰撞,球2再与球3碰撞,经上述碰撞后三个小球的动量大小之比为1∶1∶2,方向相同,且球3恰能滑出容器,求三个小球的质量之比m₁∶m₂∶m₃和h₀的值.

Answer 1

（1）球1与球2、球2与球3碰撞后交换速度，球3滑至h高处，再滑回与球2碰撞，而球2与球1碰撞，又使球1滑回h高处，此后系统将做周期性运动，又因为h＜＜R

T₁=T₃=2π①

而T=+②

由①②得T=2π.③

(2)依题意三个球碰后的动量之比为1∶1∶2,令p₁′=p，p₂′=p,p₃′=2p

由系统动量守恒得球1碰前动量

p₁=p₁′+p₂′+p₃′=4p④

由动量守恒得球1与球2碰后球2的动量

p₂=p₁-p₁′=3p⑤

碰撞时无机械能损失，则有

+⑥

由⑥式得⑦

球2与球3碰撞时动量守恒且无机械能损失，则有

⑧

由⑧式得⑨

由⑦⑨得m₁∶m₂∶m₃=10∶6∶3⑩

对球3，碰后恰滑出容器，由机械能守恒得

=m₃gR

而对球1，刚滑下直至与球2碰撞前机械能守恒，则

=m₁gh₀

解得：h₀=0.36R