
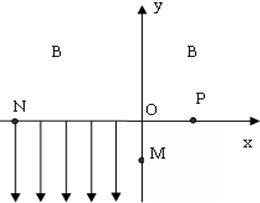
 ��ͼ��ʾ����ֱ������ϵ�ĵ�һ�����������д�ֱ��ֽ�淽�����ǿ�ų���������������y�Ḻ�������ǿ�糡�������������糡�ʹų�������Ϊm�������Ϊ-q��q��0�������Ӵ�M�����ٶ�v0��x�Ḻ�������糡���������ӵ����������Ӿ�x���ϵ�N���P���ֻص�M�㣮OM=OP=L��ON=2L����
��ͼ��ʾ����ֱ������ϵ�ĵ�һ�����������д�ֱ��ֽ�淽�����ǿ�ų���������������y�Ḻ�������ǿ�糡�������������糡�ʹų�������Ϊm�������Ϊ-q��q��0�������Ӵ�M�����ٶ�v0��x�Ḻ�������糡���������ӵ����������Ӿ�x���ϵ�N���P���ֻص�M�㣮OM=OP=L��ON=2L����| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
| Eq |
| m |
| t | 2 1 |
2m
| ||
| 4qL |
m
| ||
| 2qL |
| 0+vNy |
| 2 |
|
| 2 |
| 2 |
| 2L |
| v0 |
| 3 |
| 4 |
3
| ||
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
3
| ||
|
| 9��L |
| 4v0 |
| PM |
| vP |
| ||
|
| L |
| v0 |
| 2L |
| v0 |
| 9��L |
| 4v0 |
| L |
| v0 |
| (12+9��) |
| 4v0 |
| mv02 |
| 2qL |
| 2 |
| (12+9��) |
| 4v0 |


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�
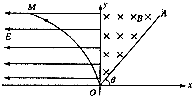 ��ͼ��ʾ����ֱ������ƽ��ĵ�I��������һ��ǿ�ų����Ÿ�Ӧǿ��ΪB��ֱ��OA�Ǵų��Ҳ�ı߽磮�ڵڢ����������ڵ糡ǿ�ȴ�СΪE��ˮƽ�������ǿ�糡��y���ǵ糡���ų�����ķֽ������ߣ�OM���㷽��x=-ky2��k��0������һ�������Ϊq������Ϊm�ĸ����ӣ��������ƣ�������OM��ijһ���ɾ�ֹ�ͷţ���Խy�����ų��У�
��ͼ��ʾ����ֱ������ƽ��ĵ�I��������һ��ǿ�ų����Ÿ�Ӧǿ��ΪB��ֱ��OA�Ǵų��Ҳ�ı߽磮�ڵڢ����������ڵ糡ǿ�ȴ�СΪE��ˮƽ�������ǿ�糡��y���ǵ糡���ų�����ķֽ������ߣ�OM���㷽��x=-ky2��k��0������һ�������Ϊq������Ϊm�ĸ����ӣ��������ƣ�������OM��ijһ���ɾ�ֹ�ͷţ���Խy�����ų��У��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��2013?������ģ����ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶȦ�0��x���������糡����y����Q���뿪�糡ʱ�ٶȱ�Ϊ2��0��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ�ľ�����ǿ�ų�����ͼ��δ���������ӹ�Q������˶�һ�ξ����Ž���ų������ų��Ÿ�Ӧǿ�ȴ�СB=
��2013?������ģ����ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶȦ�0��x���������糡����y����Q���뿪�糡ʱ�ٶȱ�Ϊ2��0��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ�ľ�����ǿ�ų�����ͼ��δ���������ӹ�Q������˶�һ�ξ����Ž���ų������ų��Ÿ�Ӧǿ�ȴ�СB=| mv0 | qd |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶ�v0��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��нǦ�=30�㣬Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�СB=
��ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶ�v0��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��нǦ�=30�㣬Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�СB=| mv0 | qd |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ����ֱ������xoy�ĵ�һ�����зֲ���ָ��y�᷽�����ǿ�糡���ڵ��������зֲ��Ŵ�ֱֽ�����﷽�����ǿ�ų���һ������Ϊm�����磫q������(��������)��A��(0��3)�Գ���V0��120m/sƽ��x������糡����Ȼ��ӵ糡�������ų����ִӴų�����糡������ֻͨ��x���ϵ�P��(6��0)��Q��(8��0)��һ�Σ���֪�����ӵĺ��ʱ�Ϊq/m��108c/kg��
��ͼ��ʾ����ֱ������xoy�ĵ�һ�����зֲ���ָ��y�᷽�����ǿ�糡���ڵ��������зֲ��Ŵ�ֱֽ�����﷽�����ǿ�ų���һ������Ϊm�����磫q������(��������)��A��(0��3)�Գ���V0��120m/sƽ��x������糡����Ȼ��ӵ糡�������ų����ִӴų�����糡������ֻͨ��x���ϵ�P��(6��0)��Q��(8��0)��һ�Σ���֪�����ӵĺ��ʱ�Ϊq/m��108c/kg��
(1)�������������ڵ糡�ʹų��е��˶��켣��
(2)��Ÿ�ǿ��B�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ��2014������������������һ��ѧ�����ϵڶ��μ�������Ծ��������棩 ���ͣ�������
��20�֣���ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶ� ��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��н�
��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��н� ��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�С
��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�С �������ܴ�����ԭ��O��x�Ḻ���ٽ���糡������������������
�������ܴ�����ԭ��O��x�Ḻ���ٽ���糡������������������

��1���糡ǿ�ȴ�СE��
��2������н���ǿ�ų�����Ϊ��Բ�Σ���ų��������С�����
��3�����Ӵ�P���˶���O�����ʱ�䣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com