甲、乙两车从同一地点同向行驶,但是甲车做匀速直线运动,其速度为v=20米/秒,乙车在甲车行驶至距离出发地200米处时开始以初速度为零、加速度为a=2米/秒2追甲.求:
(1)乙车追上甲车前两车间的最大距离.
(2)乙车追上甲车时,乙车运动了多长时间(可保留根号).
解:(1)两车相遇前距离最大时两车速度必然相等,则运动时间t为:
t=

∴△x=x
0+x
甲-x
乙=

=200+20×
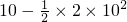
m=300m
(2)设经过时间t′后两车相遇,则有:


解得:t′=
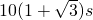
答:(1)乙车追上甲车前两车间的最大距离为300m.
(2)乙车追上甲车时,乙车运动的时间为
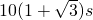
.
分析:(1)该题中两汽车运动,乙车追甲车,开始乙车初速度为零,做加速运动,甲车在前以恒定速度做匀速运动,在开始一段时间里,甲车速度较乙车速度大,不难想到,只要乙车速度小于甲车速度,两车间距离必随时间延长而增大.反之,如乙车速度在某时刻开始较甲车速度大,则两车间距离随时间延长而变小.显然当两车速度相同时距离最大.
(2)乙车追上甲车时,两车处于同一位置,根据位移和时间之间的关系即可求解.
点评:可见,在追赶过程中,速度相等是一个转折点,要熟记这一条件.在诸多的物理问题中存在“隐蔽条件”成为一个很重要的问题,一般是根据物理过程确定.该题中“隐蔽条件”就是当两车速度相同时距离最大.解析后,问题就迎刃而解.


 =200+20×
=200+20×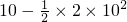 m=300m
m=300m

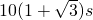
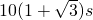 .
.
