
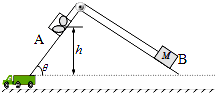
 如图所示为仓储公司常采用的“自动化”货物装卸装置,两个相互垂直的光滑斜面固定在地面上,货箱A(含货物)和配重B通过与斜面平行的轻绳跨过光滑滑轮相连.A装载货物后从h=8.0m高处由静止释放,运动到底端时,A和B同时被锁定,卸货后解除锁定,A在B的牵引下被拉回原高度处,再次被锁定.已知θ=53°,B的质量M为1.0×103kg,g取10m/s2,sin53°=0.8,cos53°=0.6.
如图所示为仓储公司常采用的“自动化”货物装卸装置,两个相互垂直的光滑斜面固定在地面上,货箱A(含货物)和配重B通过与斜面平行的轻绳跨过光滑滑轮相连.A装载货物后从h=8.0m高处由静止释放,运动到底端时,A和B同时被锁定,卸货后解除锁定,A在B的牵引下被拉回原高度处,再次被锁定.已知θ=53°,B的质量M为1.0×103kg,g取10m/s2,sin53°=0.8,cos53°=0.6.分析 (1)由题意可明确下滑的条件:货箱A的合力沿斜面向下,分析货箱的受力情况,即可求得质量m的范围;
(2)对系统应用动能定理可求得A到达底端时的速度v.
解答 解:(1)设左斜面倾角为θ,左斜面倾角为β,则β=53°
货箱由静止释放后能沿斜面下滑,则
F合>0
即 mgsinθ-Mgsinβ>0
解得 m>750kg
(2)对系统,应用动能定理得:
由动能定理:W合=△Ek
即 mgh-Mg•$\frac{h}{sinθ}$•sinβ=$\frac{1}{2}$(M+m)v2;
解得 v=3$\sqrt{10}$m/s
答:
(1)为使A由静止释放后能沿斜面下滑,其质量m需要满足的条件是:m>750kg.
(2)若A的质量m=3.0×103kg,它到达底端时的速度v是3$\sqrt{10}$m/s.
点评 本题考查动能定理、牛顿第二定律的应用,要注意正确分析题意,明确物理过程,应用动能定理研究.运用动能定理时,也可以采用隔离法分别列式.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中物理 来源: 题型:填空题
 如图所示,弯折的直角轻杆ABCO通过铰链O连接在地面上,AB=BC=OC=9m,一质量为m的小滑块以足够大的初始速度,在杆上从C点左侧x0=2m处向左运动,作用于A点的水平向右拉力F可以保证BC始终水平.若滑块与杆之间的动摩擦因数与离开C点的距离x满足μx=1,则滑块的运动位移s=3m时拉力F达到最小.若滑块的初始速度v0=5m/s,且μ=0.5-0.1x(μ=0后不再变化),则滑块达到C点左侧x=4m处时,速度减为v=1m/s.
如图所示,弯折的直角轻杆ABCO通过铰链O连接在地面上,AB=BC=OC=9m,一质量为m的小滑块以足够大的初始速度,在杆上从C点左侧x0=2m处向左运动,作用于A点的水平向右拉力F可以保证BC始终水平.若滑块与杆之间的动摩擦因数与离开C点的距离x满足μx=1,则滑块的运动位移s=3m时拉力F达到最小.若滑块的初始速度v0=5m/s,且μ=0.5-0.1x(μ=0后不再变化),则滑块达到C点左侧x=4m处时,速度减为v=1m/s.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 图甲是某研究者在地面上拍摄的小球做自由落体运动的频闪照片.假设在月球上使用相同的设备,并保持频闪光源闪光的时间间隔不变,拍摄小球在月球表面做自由落体运动的频闪照片,可能是图乙中的C.
图甲是某研究者在地面上拍摄的小球做自由落体运动的频闪照片.假设在月球上使用相同的设备,并保持频闪光源闪光的时间间隔不变,拍摄小球在月球表面做自由落体运动的频闪照片,可能是图乙中的C.查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 某同学在“用单摆测重力加速度”的实验中,把摆球用细线悬挂在铁架台上,测量摆线长摆球直径,通过计算得到摆长L.
某同学在“用单摆测重力加速度”的实验中,把摆球用细线悬挂在铁架台上,测量摆线长摆球直径,通过计算得到摆长L.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 线速度大 | B. | 角速度大 | C. | 周期大 | D. | 向心加速度大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 月球表面的重力加速度为$\frac{4{π}^{2}(R+h)^{3}}{{T}^{2}{R}^{2}}$ | |
| B. | 月球表面的重力加速度为$\frac{4{π}^{2}(R+h)}{{T}^{2}}$ | |
| C. | LRO运行时的向心加速度为$\frac{4{π}^{2}R}{{T}^{2}}$ | |
| D. | LRO运行时的向心加速度为$\frac{4{π}^{2}(R+h)^{2}}{{T}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com