
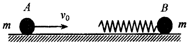
 如图所示,光滑水平面上,质量为m的小球B连接着轻质弹簧,处于静止状态;质量也为m的小球A以某一速度向右匀速运动,已知碰撞过程中总机械能守恒,两球距离最近时弹簧的弹性势能为EP,则碰前A球的速度为2$\sqrt{\frac{{E}_{p}}{m}}$.
如图所示,光滑水平面上,质量为m的小球B连接着轻质弹簧,处于静止状态;质量也为m的小球A以某一速度向右匀速运动,已知碰撞过程中总机械能守恒,两球距离最近时弹簧的弹性势能为EP,则碰前A球的速度为2$\sqrt{\frac{{E}_{p}}{m}}$. 分析 当弹簧压缩至最短时,两球的速度相等,据题此时弹簧的弹性势能为Ep,根据系统的动量守恒和机械能守恒列式,即可求出碰撞前A球的速度.
解答 解:当弹簧压缩到最短时,A、B的速度相等,设为v.
取向右为正方向,根据动量守恒定律得
mv0=2mv①
A和B的共同速度:v=0.5v0
根据系统的机械能守恒得:$\frac{1}{2}$mv02=$\frac{1}{2}$•2mv2+Ep,
联立解得,${v_0}=2\sqrt{\frac{E_p}{m}}$
故答案为:2$\sqrt{\frac{{E}_{p}}{m}}$.
点评 本题是含有弹簧的问题,关键要掌握两球最近的临界角条件:速度相等,抓住系统的动量守恒和机械能守恒进行分析.


科目:高中物理 来源: 题型:解答题
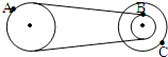 如图所示的皮带传动装置中,右边两轮粘在一起且同轴,A、B、C三点均是各轮边缘上的一点,半径RA=RC=2RB,皮带不打滑,则:线速度vA:vB:vC=1:1:2;向心加速度aA:aB:aC=1:2:4.
如图所示的皮带传动装置中,右边两轮粘在一起且同轴,A、B、C三点均是各轮边缘上的一点,半径RA=RC=2RB,皮带不打滑,则:线速度vA:vB:vC=1:1:2;向心加速度aA:aB:aC=1:2:4.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
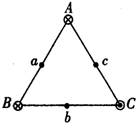 正三角形ABC的三个顶点处分别有垂直于三角形平面的无限长直导线,导线中通有恒定电流,方向如图所示,a、b、c三点分别是正三角形三边的中点,若A、B、C三处导线中的电流分别为I、2I、3I,已知无限长直导线在其周围某一点产生的磁场磁感应强度B的大小与电流成正比,与电流到这一点的距离成反比,即B=k$\frac{I}{r}$,则a、b、c三点的磁感应强度大小关系为( )
正三角形ABC的三个顶点处分别有垂直于三角形平面的无限长直导线,导线中通有恒定电流,方向如图所示,a、b、c三点分别是正三角形三边的中点,若A、B、C三处导线中的电流分别为I、2I、3I,已知无限长直导线在其周围某一点产生的磁场磁感应强度B的大小与电流成正比,与电流到这一点的距离成反比,即B=k$\frac{I}{r}$,则a、b、c三点的磁感应强度大小关系为( )| A. | a点最大 | B. | b点最大 | C. | c点最大 | D. | b、c两点一样大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
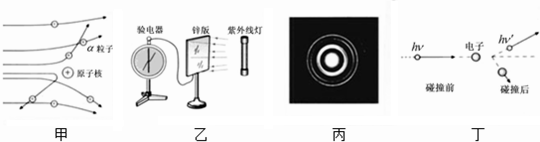
| A. | 甲图和丙图对应的实验,说明了原子内部是非常空旷的,并可以据此估算出原子核的大小 | |
| B. | 通过乙图和丁图对应的实验,用碰撞模型对实验现象做出了解释,使认识到光子具有能量和动量,说明光具有粒子性 | |
| C. | 通过乙图对应的实验,提出光子说,但在认为光有粒子性的同时,并没有否定光的波动性,因为光子的能量E=hν,其中ν为光的频率--这是描述波的物理量之一 | |
| D. | 通过丙图对应的实验,发现电子具有波动性,其波长和动量的关系为λ=hp |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 4m/s | B. | 5m/s | C. | 10m/s | D. | 50m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 四颗星围绕正方形对角线的交点做匀速圆周运动 | |
| B. | 四颗星的线速度均为$\sqrt{\frac{Gm}{a}(2+\frac{\sqrt{2}}{4})}$ | |
| C. | 四颗星表面的重力加速度均为$\frac{Gm}{{R}^{2}}$ | |
| D. | 四颗星的周期均为2πa$\sqrt{\frac{2a}{(4+\sqrt{2})Gm}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com