
| A. | 0.58 | B. | 0.87 | C. | 1.1 | D. | 2.4 |
分析 飞船受万有引力提供向心力,根据牛顿第二定律列式求解出周期表达式进行分析即可.
解答 解:飞船受万有引力提供向心力,故:
$mg=m\frac{4{π}^{2}}{{T}^{2}}r$
解得:
T=2π$\sqrt{\frac{r}{g}}$;
设地球表示重力加速度为g,半径为R,则地球表面附近绕地球沿圆轨道运行的人造卫星周期为:
T2=2π$\sqrt{\frac{R}{g}}$;
某一飞船绕“581C”行星做匀速圆周运动,其轨道半径等于该行星的直径,运动周期为:
T1=2π$\sqrt{\frac{r}{g′}}$
其中:r=3R,
根据g=$\frac{GM}{{r}^{2}}$,g′=$\frac{1}{4}{g}_{0}=\frac{1}{2}g$
故T1=2π$\sqrt{\frac{3R}{\frac{1}{2}g}}$;
故$\frac{{T}_{1}}{{T}_{2}}=\sqrt{6}$≈2.4
故选:D.
点评 本题涉及两个物理模型:飞船做圆周运动的向心力由万有引力提供;在星球表面,重力等于万有引力;基础题目.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,MNP为竖直面内一固定轨道,其光滑圆弧段MN为半径为R的$\frac{1}{4}$圆弧,与粗糙水平段NP相切于N.P端固定一竖直挡板.NP长度为L.一质量为m小木块(可视为质点)自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞后停止在距P点距离为S的水平轨道上.重力加速度为g.求:
如图,MNP为竖直面内一固定轨道,其光滑圆弧段MN为半径为R的$\frac{1}{4}$圆弧,与粗糙水平段NP相切于N.P端固定一竖直挡板.NP长度为L.一质量为m小木块(可视为质点)自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞后停止在距P点距离为S的水平轨道上.重力加速度为g.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
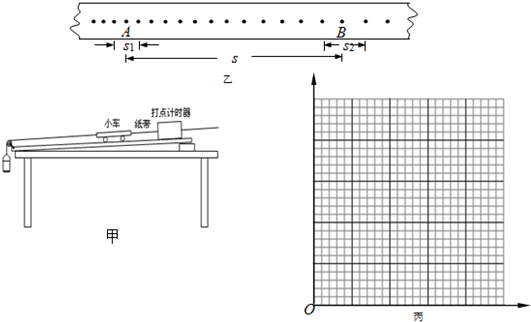
| 次数 | 小车质量 M/g | 加速度 a/m•s-2 | $\frac{1}{M}$/kg-1 |
| 1 | 200 | 1.91 | 5.00 |
| 2 | 250 | 1.71 | 4.00 |
| 3 | 300 | 1.50 | 3.33 |
| 4 | 350 | 1.36 | 2.86 |
| 5 | 400 | 1.12 | 2.50 |
| 6 | 450 | 1.00 | 2.22 |
| 7 | 500 | 0.90 | 2.00 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
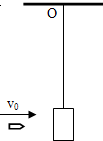 如图一砂袋用无弹性轻细绳悬于O点.开始时砂袋处于静止状态,此后用弹丸以水平速度击中砂袋后均未穿出.第一次弹丸的速度为v0,打入砂袋后二者共同摆动的最大摆角为θ(θ<90°),当其第一次返回图示位置时,第二粒弹丸以另一水平速度v又击中砂袋,使砂袋向右摆动且最大摆角仍为θ.若弹丸质量均为m,砂袋质量为4m,弹丸和砂袋形状大小忽略不计,求:两粒弹丸的水平速度之比$\frac{v_0}{v}$为多少?
如图一砂袋用无弹性轻细绳悬于O点.开始时砂袋处于静止状态,此后用弹丸以水平速度击中砂袋后均未穿出.第一次弹丸的速度为v0,打入砂袋后二者共同摆动的最大摆角为θ(θ<90°),当其第一次返回图示位置时,第二粒弹丸以另一水平速度v又击中砂袋,使砂袋向右摆动且最大摆角仍为θ.若弹丸质量均为m,砂袋质量为4m,弹丸和砂袋形状大小忽略不计,求:两粒弹丸的水平速度之比$\frac{v_0}{v}$为多少?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
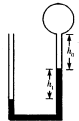 如图所示,竖直放置且粗细均匀的U形玻璃管与容积为V0=90cm3的金属球形容器连通,用U形玻璃管中的水银柱封闭一定质量的理想气体,当环境温度为27℃时,U形玻璃管右侧水银面比左侧水银面高出h1=16cm,水银柱上方空气长h0=20cm.现在对金属球形容器缓慢加热,当U形玻璃管左侧水银面比右侧水银面高出h2=24cm时停止加热,求此时金属球形容器内气体的温度为多少摄氏度?已知大气压P0=76cmHg,U形玻璃管的横截面积为S=0.5cm2.
如图所示,竖直放置且粗细均匀的U形玻璃管与容积为V0=90cm3的金属球形容器连通,用U形玻璃管中的水银柱封闭一定质量的理想气体,当环境温度为27℃时,U形玻璃管右侧水银面比左侧水银面高出h1=16cm,水银柱上方空气长h0=20cm.现在对金属球形容器缓慢加热,当U形玻璃管左侧水银面比右侧水银面高出h2=24cm时停止加热,求此时金属球形容器内气体的温度为多少摄氏度?已知大气压P0=76cmHg,U形玻璃管的横截面积为S=0.5cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com