
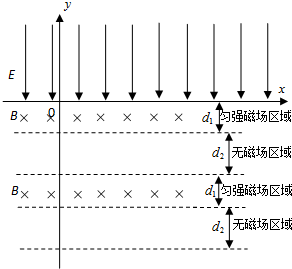
分析 (1)粒子在电场中加速,根据动能定理可以得到速度的大小;
(2)由动能定理求出粒子的速度,由牛顿第二定律可以正确解题.
(3)由动能定理求出粒子的速度,由运动学公式与牛顿第二定律、公式t=$\frac{θ}{2π}$T可以求出运动时间.
解答 解:(1)由$Eq{h_1}=\frac{1}{2}mv_1^2$
得到${v_1}=\sqrt{\frac{{2Eq{h_1}}}{m}}=5×{10^2}m/s$
(2)粒子经电场加速,经过x轴时速度大小为v,满足:$Eqh=\frac{1}{2}mv_{\;}^2$
之后进入下方磁场区,依据题意可知运动半径应满足:R1<d1
又由$qvB=m\frac{v^2}{R_1}$
得${R_1}=\frac{{m{v_1}}}{qB}$
由以上三式可得:${h_1}<\frac{{q{B^2}d_1^2}}{2Em}=1.8×{10^{-2}}m$
(3)当粒子从h2=5cm的位置无初速释放后,先在电场中加速,
加速时间为t1满足${h_2}=\frac{1}{2}\frac{Eq}{m}t_1^2$
解得 ${t_1}=\sqrt{\frac{{2{h_2}m}}{Eq}}=1×{10^{-4}}s$
进入磁场的速度大小为v2,圆周运动半径为R2
$Eq{h_2}=\frac{1}{2}mv_2^2$
解得 ${v_2}=\sqrt{\frac{{2Eq{h_2}}}{m}}=1×{10^3}m/s$
${R_2}=\frac{{m{v_2}}}{qB}$
解得:${R_2}=\frac{{\sqrt{2Em{h_2}}}}{{\sqrt{q}B}}=5cm$
根据粒子在空间运动轨迹可知,它最低能进入第二个磁场区
它在磁场区共运动时间为半个圆周运动的时间${t_2}=\frac{πm}{qB}=1.57×{10^{-4}}s$
它经过第一无磁场区时运动方向与x轴的夹角θ满足:$sinθ=\frac{d_1}{R_2}=0.6$
所以它在无磁场区的路程$s=\frac{{2{d_2}}}{cosθ}=0.1m$
无磁场区运动时间${t_3}=\frac{s}{v_2}=1×{10^{-4}}s$
总时间$t={t_1}+{t_2}+{t_3}=3.57×{10^{-4}}s$
答:
(1)粒子刚刚进入磁场瞬间的速度大小为500m/s.
(2)h应小于1.8×10-2m;
(3)粒子自释放到第二次过x轴的时间为3.57×10-4s.
点评 本题考查了带电粒子在电磁场中的运动,是电磁学综合题,分析清楚粒子运动过程是正确解题的前提与关键,应用动能定理、牛顿第二定律、运动学公式即可正确解题.


科目:高中物理 来源: 题型:选择题
| A. | 速度越大牵引力越大 | B. | 速度越大牵引力越小 | ||
| C. | 牵引力与速度无关 | D. | 以上说法都不对 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 某兴趣小组准备探究“合外力做功和物体速度变化的关系”,实验前组员们提出了以下几种猜想:
某兴趣小组准备探究“合外力做功和物体速度变化的关系”,实验前组员们提出了以下几种猜想:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 电能是我们社会生活的重要资源,由于地理环境的限制,发电站一般离用电的场所都很远.现假设将三门核电站(如图所示)发出来的电输送到椒江使用,在远距离输电过程中,一定要考虑输送效率问题,下列说法正确的是( )
电能是我们社会生活的重要资源,由于地理环境的限制,发电站一般离用电的场所都很远.现假设将三门核电站(如图所示)发出来的电输送到椒江使用,在远距离输电过程中,一定要考虑输送效率问题,下列说法正确的是( )| A. | 高压输电是通过减小输电电流来减小电路的发热损耗 | |
| B. | 减小输电线的电阻有利于减少输电过程中的电能损失 | |
| C. | 增大输电线的电阻有利于减小输电过程中的电能损失 | |
| D. | 在输送电压一定时,输送的电功率越大,输电过程中的电能损失越小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题
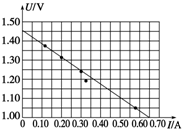 在用电压表和电流表测电池的电动势和内阻的实验中一位同学在图中画出U-I图象,根据图象读出电池的电动势E=1.46 V,求出电池的内阻r=0.708Ω.(保留三位有效数字)
在用电压表和电流表测电池的电动势和内阻的实验中一位同学在图中画出U-I图象,根据图象读出电池的电动势E=1.46 V,求出电池的内阻r=0.708Ω.(保留三位有效数字)查看答案和解析>>
科目:高中物理 来源: 题型:实验题
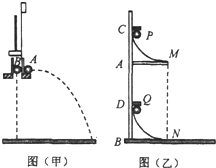 ①某同学在“探究平抛运动的规律”的实验中,先采用图(甲)所示装置,用小锤打击弹性金属片,金属片把球A沿水平方向弹出,同时B球被松开,自由下落,观察到两球同时落地,改变小捶打击的力度,即改变球A被弹出时的速度,两球仍然同时落地,这说明平抛运动的竖直分运动是自由落体运动.
①某同学在“探究平抛运动的规律”的实验中,先采用图(甲)所示装置,用小锤打击弹性金属片,金属片把球A沿水平方向弹出,同时B球被松开,自由下落,观察到两球同时落地,改变小捶打击的力度,即改变球A被弹出时的速度,两球仍然同时落地,这说明平抛运动的竖直分运动是自由落体运动.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,直角坐标系xoy位于竖直平面内,在$-\sqrt{3}$m≤x≤0的区域内有磁感应强度大小B=4.0×10-2T、方向垂直于纸面向里的匀强磁场,其左边界与x轴交于P点;在x>0的某区域内有电场强度大小E=3.2×104N/C、方向沿y轴正方向的有界匀强电场,其宽度d=2m.一质量m=4.0×10-25kg、电荷量q=-2.0×10-17C的带电粒子从P点以速度v=4.0×106m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力.求:
如图所示,直角坐标系xoy位于竖直平面内,在$-\sqrt{3}$m≤x≤0的区域内有磁感应强度大小B=4.0×10-2T、方向垂直于纸面向里的匀强磁场,其左边界与x轴交于P点;在x>0的某区域内有电场强度大小E=3.2×104N/C、方向沿y轴正方向的有界匀强电场,其宽度d=2m.一质量m=4.0×10-25kg、电荷量q=-2.0×10-17C的带电粒子从P点以速度v=4.0×106m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
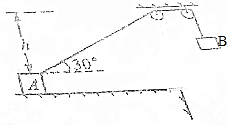 物体A的质量为10kg,置于光滑水平面上,物体B的这两位1kg,用轻绳通过两等高的定滑轮与A连接,如图所示,h=0.5m,A、B由图示位置从静止释放,忽略绳与滑轮间的摩擦,求运动中A的最大速度vA=?.
物体A的质量为10kg,置于光滑水平面上,物体B的这两位1kg,用轻绳通过两等高的定滑轮与A连接,如图所示,h=0.5m,A、B由图示位置从静止释放,忽略绳与滑轮间的摩擦,求运动中A的最大速度vA=?.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com