
 ��ͼ��ʾ��xOyƽ��Ϊ�⻬ˮƽ�棬����һ��Ϊd��ΪL�ĵ����߿�MNPQ������F�����£���x�����������ٶ�v������ֱ���˶����ռ������ֱ����Ĵų����Ÿ�Ӧǿ��B=B0cos$\frac{��}{d}$x��ʽ��B0Ϊ��֪�������涨��ֱ���·���Ϊ�Ÿ�Ӧǿ���������߿����ΪR��t=0ʱ��MN��ǡ����y�ᴦ����
��ͼ��ʾ��xOyƽ��Ϊ�⻬ˮƽ�棬����һ��Ϊd��ΪL�ĵ����߿�MNPQ������F�����£���x�����������ٶ�v������ֱ���˶����ռ������ֱ����Ĵų����Ÿ�Ӧǿ��B=B0cos$\frac{��}{d}$x��ʽ��B0Ϊ��֪�������涨��ֱ���·���Ϊ�Ÿ�Ӧǿ���������߿����ΪR��t=0ʱ��MN��ǡ����y�ᴦ�������� ��1�������ֶ��ж�ͨ���߿�MNPQ�ĵ��������ݱպϵ�·��ŷķ���ɺͷ����ڵ�Ÿ�Ӧ��������Ӧ������С��
��2������e=2BLv����˶��������߿�MNPQ�ĵ綯�Ʊ���ʽ�����ݱպϵ�·��ŷķ����������ǿ�ȱ���ʽ���������밲�����Ĺ�ϵ���ɵõ�����F��λ��x�Ĺ�ϵʽ��
��3������˲ʱ���������ҹ��ɱ仯�������Ӧ��������Чֵ���ٸ��ݽ������������Ȧ�в����ĵ��ȣ�
��� �⣺��1��t=0ʱ�̣������ֶ���֪��ͨ���߿�MNPQ�ĵ���Ϊ˳ʱ�뷽��t=0ʱ�̣��߿�MNPQ�ĵ綯��Ϊ��
E0=2B0Lv
�߿�MNPQ�ĵ�����СΪ��
${I_0}=\frac{E_0}{R}$
������ã�${I_0}=\frac{{2{B_0}Lv}}{R}$��
��2���˶��������߿�MNPQ�ĵ綯��Ϊ��
$e=2BLv=2{B_0}Lvcos\frac{��}{d}x$
ͨ���߿�MNPQ�ĵ�����СΪ��
$i=\frac{e}{R}=\frac{{2{B_0}Lv}}{R}cos\frac{��}{d}x$
�߿�PQ���ܵ���������СΪ��
F��=BiL
������СΪ��F=2F��
������ã�$F=\frac{{4B_0^2{L^2}v}}{R}{cos^2}��\frac{��}{d}x��$��
��3������˲ʱ���������ҹ��ɱ仯���ʿ�֪��Ӧ��������ЧֵΪ��
$I=\frac{i_m}{{\sqrt{2}}}=\frac{{2{B_0}Lv/R}}{{\sqrt{2}}}=\frac{{\sqrt{2}{B_0}Lv}}{R}$
���Ծ���$t=\frac{d}{v}$����Ȧ�в����ĵ���Ϊ��
$Q={I^2}Rt=\frac{{2B_0^2{L^2}dv}}{R}$��
�𣺣�1��t=0ʱ�̣�ͨ���߿�MNPQ�ĵ�����СΪ$\frac{2{B}_{0}Lv}{R}$������Ϊ˳ʱ�뷽��
��2������F��λ��x�Ĺ�ϵʽΪ$F=\frac{4{B}_{0}^{2}{L}^{2}v}{R}co{s}^{2}��\frac{��}{d}x��$��
��3������t=$\frac{d}{v}$����Ȧ�в����ĵ���Ϊ$\frac{2{B}_{0}^{2}{L}^{2}dv}{R}$��
���� ���ڵ�Ÿ�Ӧ�����о�˼·������������һ�������ĽǶȣ��ص��Ƿ��������������µ������ƽ�����⣬����ƽ�������г����̣���һ���������������漰��Ÿ�Ӧ�����е�����ת�����⣬���ݶ��ܶ��������ܹ�ϵ���з�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ��1����ͼ��ʾ���о�ƽ�������˶�����ʾʵ��װ�ã�ʵ��ʱ�����õ���ƬC��B���ѹ��DE�䲢��A����ͬһˮƽ���ϣ���С��F����ƬC��A��ˮƽ�׳���ͬʱB���������䣮ʵ�鼸�Σ����۴�������С��������������ͣ���������A��B��������ͬʱ��أ����ʵ��D
��1����ͼ��ʾ���о�ƽ�������˶�����ʾʵ��װ�ã�ʵ��ʱ�����õ���ƬC��B���ѹ��DE�䲢��A����ͬһˮƽ���ϣ���С��F����ƬC��A��ˮƽ�׳���ͬʱB���������䣮ʵ�鼸�Σ����۴�������С��������������ͣ���������A��B��������ͬʱ��أ����ʵ��D�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | С����ߵ���ٶ�Ϊ0 | |
| B�� | С����ߵ���ٶ�Ϊ$\sqrt{gR}$ | |
| C�� | С����ߵ��ܵ��ĵ���Ϊ0 | |
| D�� | С������͵��ܵ��ĵ������ܵ������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ijʵ��С����ͼʾװ��̽��Ӱ��ƽ�а���������ݵ����أ����������������ΪS�������ľ���Ϊd�������ָ��ƫ��Ϊ�ȣ�ʵ���У��ٶ�����������������䣬�����ж�����ȷ���ǣ�������
ijʵ��С����ͼʾװ��̽��Ӱ��ƽ�а���������ݵ����أ����������������ΪS�������ľ���Ϊd�������ָ��ƫ��Ϊ�ȣ�ʵ���У��ٶ�����������������䣬�����ж�����ȷ���ǣ�������| A�� | ����S���䣬����d����C��С���ȱ�� | B�� | ����S���䣬����d����C��ȱ�С | ||
| C�� | ����d���䣬��СS����C��С���ȱ�� | D�� | ����d���䣬��СS����C��ȱ�С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
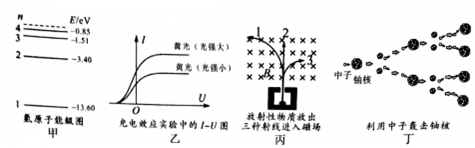
| A�� | ��ͼ�У�һȺ����n=4�ܼ�����ԭ��ԾǨ��n=1�ܼ��Ĺ����пɷ���8�в�ͬƵ�ʵĹ��� | |
| B�� | ��ͼ�У��ڹ���ɫ���ֲ��������£������Խǿ���������Խ�� | |
| C�� | ��ͼ�У�1Ϊ�����ߣ�2Ϊ�����ߣ�3Ϊ������ | |
| D�� | ��ͼ�У��˷�Ӧ������˾۱� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ¬ɪ��ͨ���Ԧ�����ɢ��ʵ�����ķ����������ԭ�Ӻ��������Ӵ��� | |
| B�� | ��й©�¹���Ⱦ��137CS�ܹ������������к��ķ��䣬��˷�Ӧ����ʽΪ${\;}_{55}^{137}{C_S}��{\;}_{56}^{137}{B_a}+x$�������ж�xΪ���� | |
| C�� | ����ԭ�Ӵ�n=6�ܼ���n=1�ܼ�ԾǨʱ������Ĺⲻ��ʹij�����������ЧӦ������ԭ�Ӵ�n=6�ܼ���n=2�ܼ�ԾǨʱ������Ĺ�Ҳ����ʹ�ý����������ЧӦ | |
| D�� | ���ӡ����ӡ������ӵ������ֱ��� m1��m2��m3�����Ӻ����ӽ�ϳ�һ�������ӣ��ͷŵ�������$��{{2m}_1+{2m}_2-m_3}��c^2$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 뱵İ�˥����3.8�죬����10���ԭ�Ӻ˾���3.8��һ����ʣ5�� | |
| B�� | ̫�������������Ҫ����̫���ڲ��ĺ��ѱ䷴Ӧ | |
| C�� | ����ƾ����������һ��ԭ�Ӻ� | |
| D�� | �¶�Խ�ߣ�������Ԫ��˥��Խ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ��ˮƽ���õĹ⻬ƽ�н�����������費�ƣ�������ΪL=2m�������������һ��ֵΪR=6���ĵ��裮������ڴ洹ֱ���ƽ�����µ��н���ǿ�ų���һ����Ϊm������Ϊr=2���Ľ�����MN���ڵ����ϣ��뵼�촹ֱ�ҽӴ����ã��ܵ�F=0.2v+3��N����vΪ�������ٶȣ���ˮƽ�������ã��Ӵų�����߽��ɾ�ֹ��ʼ�˶����õ�ѹ����õ������˵�ѹ��ʱ���������
��ͼ��ʾ��ˮƽ���õĹ⻬ƽ�н�����������費�ƣ�������ΪL=2m�������������һ��ֵΪR=6���ĵ��裮������ڴ洹ֱ���ƽ�����µ��н���ǿ�ų���һ����Ϊm������Ϊr=2���Ľ�����MN���ڵ����ϣ��뵼�촹ֱ�ҽӴ����ã��ܵ�F=0.2v+3��N����vΪ�������ٶȣ���ˮƽ�������ã��Ӵų�����߽��ɾ�ֹ��ʼ�˶����õ�ѹ����õ������˵�ѹ��ʱ����������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������Ϊ��ԭ���е��ӹ�������ӻ��ģ�����Ҳ�����ӻ��� | |
| B�� | ���Ӳ����������Ͷ��� | |
| C�� | ��������ԭ�Ӻ�����Ӹ����˶��γɵ� | |
| D�� | ���������䵽����п�����ʱ�ܹ����ЧӦ�������������ߵ�����ǿ��ʱ����п������ݳ��Ĺ���ӵ���������Ҳ��֮���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com