
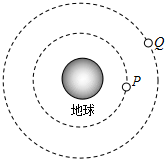
 人造地球卫星P绕地球球心作匀速圆周运动,距地球球心的距离为r,地球的质量为M,引力常量为G.
人造地球卫星P绕地球球心作匀速圆周运动,距地球球心的距离为r,地球的质量为M,引力常量为G.分析 (1)根据万有引力提供向心力,求出卫星P绕地球运动的周期.
(2)根据周期的关系求出卫星Q的轨道半径,当P、Q、地球共线且P、Q位于地球同侧时最近.
(3)根据两卫星的周期关系,求出三者共线经历的时间.
解答 解:(1)根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,卫星P绕地球运行的周期T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$;
(2)Q绕地球运行的周期是卫星P绕地球运行周期的8倍,根据T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$知,rQ=4r,
P、Q、地球共线且P、Q位于地球同侧时最近,最近距离d=4r-r=3r.
(3)当卫星P和Q同向绕行时,设经过t时间三者共线,有:$\frac{2π}{{T}_{p}}t-\frac{2π}{{T}_{Q}}t=nπ$,
解得t=$\frac{8nπ}{7}\sqrt{\frac{{r}^{3}}{GM}}$,(n=1、2、3…)
当卫星P和Q反向绕行时,设经过t时间三者共线,有:$\frac{2π}{{T}_{p}}t+\frac{2π}{{T}_{Q}}t=nπ$,
解得t=$\frac{8nπ}{9}\sqrt{\frac{{r}^{3}}{GM}}$.
答:(1)卫星P绕地球运行周期为$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$;
(2)卫星P、Q在绕地球运行过程中,两星间相距最近时的距离为3r;
(3)同向绕行时,经历的时间为t=$\frac{8nπ}{7}\sqrt{\frac{{r}^{3}}{GM}}$,(n=1、2、3…),反向绕行时,经历的时间t=$\frac{8nπ}{9}\sqrt{\frac{{r}^{3}}{GM}}$,(n=1、2、3…).
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,知道周期与轨道半径的关系,结合转过的角度关系求出共线的时间,难度中等.


科目:高中物理 来源: 题型:解答题
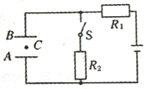 如图所示电路,电源内阻r=1Ω,电阻R1=4Ω,A、B是水平放置的平行板电容器,当开关S断开时,一电子从A板由静止飞到B板时的速度为v0,当开关S闭合时,电子从A由静止飞到B板的过程中,通过两板的中点C的速度为$\frac{\sqrt{3}}{3}$v0,求R2的阻值.
如图所示电路,电源内阻r=1Ω,电阻R1=4Ω,A、B是水平放置的平行板电容器,当开关S断开时,一电子从A板由静止飞到B板时的速度为v0,当开关S闭合时,电子从A由静止飞到B板的过程中,通过两板的中点C的速度为$\frac{\sqrt{3}}{3}$v0,求R2的阻值.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 转笔(Pen Spinning)是一项用不同的方法与技巧、以手指来转动笔的休闲活动,如图所示.转笔深受广大中学生的喜爱,其中也包含了许多的物理知识,假设某转笔高手能让笔绕其上的某一点O做匀速圆周运动,下列有关该同学转笔中涉及到的物理知识的叙述正确的是( )
转笔(Pen Spinning)是一项用不同的方法与技巧、以手指来转动笔的休闲活动,如图所示.转笔深受广大中学生的喜爱,其中也包含了许多的物理知识,假设某转笔高手能让笔绕其上的某一点O做匀速圆周运动,下列有关该同学转笔中涉及到的物理知识的叙述正确的是( )| A. | 笔杆上的点离O点越近的,角速度越大 | |
| B. | 笔杆上的点离O点越近的,做圆周运动的向心加速度越大 | |
| C. | 笔杆上的各点做圆周运动的向心力是由万有引力提供的 | |
| D. | 若该同学使用中性笔,笔尖上的小钢珠有可能因快速的转动做离心运动被甩走 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量m=1kg的小物块(质点)以水平初速度v0=12m/s自水平地面上的A点向右滑行,从点B处冲上固定无限长斜面BC(假设在B处小物块无动能损失),斜面倾角θ=37°(sin 37°=0.6,cos 37°=0.8,g=10m/s2).已知A、B两点的距离L=4.4m,小物块与各接触面的动摩擦因数都是μ=0.5,求:
如图所示,质量m=1kg的小物块(质点)以水平初速度v0=12m/s自水平地面上的A点向右滑行,从点B处冲上固定无限长斜面BC(假设在B处小物块无动能损失),斜面倾角θ=37°(sin 37°=0.6,cos 37°=0.8,g=10m/s2).已知A、B两点的距离L=4.4m,小物块与各接触面的动摩擦因数都是μ=0.5,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
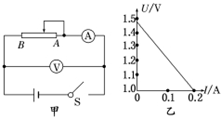 为了测量一节干电池的电动势和内阻,某实验小组按图甲所示的电路图连好实验电路,合上开关,电流表和电压表的均有读数.当将滑动变阻器的滑片由A端向B端逐渐滑动时,开始一段时间内,发现电流表的示数一直都很小,而电压表的示数接近1.5V且几乎不变,直到当滑片滑至临近B端时,电压表和电流表的示数才急剧变化,出现上述情况的原因是滑动变阻器的全阻值太大;有效使用的部分短.改进方法是换用全阻值小的滑动变阻器.改进后,测出几组电流、电压的数值,并画出如图乙所示的图象,由图象可知,这个电池的电动势为E=1.46V,内阻r=2.3Ω.
为了测量一节干电池的电动势和内阻,某实验小组按图甲所示的电路图连好实验电路,合上开关,电流表和电压表的均有读数.当将滑动变阻器的滑片由A端向B端逐渐滑动时,开始一段时间内,发现电流表的示数一直都很小,而电压表的示数接近1.5V且几乎不变,直到当滑片滑至临近B端时,电压表和电流表的示数才急剧变化,出现上述情况的原因是滑动变阻器的全阻值太大;有效使用的部分短.改进方法是换用全阻值小的滑动变阻器.改进后,测出几组电流、电压的数值,并画出如图乙所示的图象,由图象可知,这个电池的电动势为E=1.46V,内阻r=2.3Ω.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
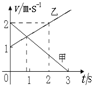
| A. | 甲、乙两物体都做匀变速直线运动 | B. | 0~1s内甲和乙的位移相同 | ||
| C. | 甲和乙的加速度方向相同 | D. | 甲和乙的运动方向相反 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
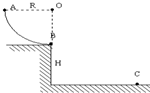 如图所示,质量为10kg的小球,从竖直圆弧轨道的A点由静止释放,沿$\frac{1}{4}$圆弧轨道运动至最低点B后飞出,落在水平面上的C点,已知圆弧半径为R=12m,小球落到C点时速度的大小为 vC=25m/s,B点离水平面高度为H=20m,不计空气阻力,g取10m/s2,求:
如图所示,质量为10kg的小球,从竖直圆弧轨道的A点由静止释放,沿$\frac{1}{4}$圆弧轨道运动至最低点B后飞出,落在水平面上的C点,已知圆弧半径为R=12m,小球落到C点时速度的大小为 vC=25m/s,B点离水平面高度为H=20m,不计空气阻力,g取10m/s2,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com