
| A�� | $\frac{\sqrt{{k}^{2}-1}}{k}$v | B�� | v$\sqrt{1-{k}^{2}}$ | C�� | v$\sqrt{{k}^{2}+1}$ | D�� | $\frac{\sqrt{1+{k}^{2}}}{k}$v |
���� ���ݴ�ͷָ��ʼ����Ӱ���ֱ������˶�ѧ��ʽ�����г��ӿ��봬�ٵĹ�ϵʽ����·����Ӱ���ֱʱ������������ӵĺ��ٶȣ��Ӷ��г��ӿ��봬�ٶȵĹ�ϵ������������⣮
��� �⣺���ˮ���ٶ�Ϊvs��
����ͷָ��ʼ����Ӱ���ֱ�����У�tȥ=$\frac{d}{{v}_{c}}$=$\frac{d}{v}$��
���س�ʱ��ʻ·����Ӱ���ֱ�����У�t��=$\frac{d}{{v}_{��}}$��
����ͷʱ�Ĵ��ĺ��ٶ�Ϊ��v��=$\sqrt{{v}^{2}-{v}_{s}^{2}}$��
����ȥ����س�����ʱ��ı�ֵΪk������С���ھ�ˮ�е��ٶȴ�СΪ��v=$\sqrt{\frac{{v}_{s}^{2}}{1-{k}^{2}}}$��
��ôˮ�����ٶ�Ϊvs=$\frac{\sqrt{{k}^{2}-1}}{k}v$����A��ȷ��BCD����
��ѡ��A��
���� �������Ĺؼ�֪�����˶�����˶����е�ʱ�ԣ��Լ�֪�������˶����ж����ԣ��������ţ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �¶ȴ����� | B�� | ������� | C�� | ���������� | D�� | ʪ�ȴ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ����ΪL�����Ϊ�ȵĹ⻬��Եб�洦�ڵ糡�У�һ������Ϊ+q������Ϊm��С���Գ��ٶ�v0��б��˵�A�㿪ʼ��б���ϻ�������б�涥��B���ٶ�ҲΪv0����
��ͼ��ʾ����ΪL�����Ϊ�ȵĹ⻬��Եб�洦�ڵ糡�У�һ������Ϊ+q������Ϊm��С���Գ��ٶ�v0��б��˵�A�㿪ʼ��б���ϻ�������б�涥��B���ٶ�ҲΪv0�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
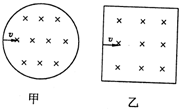 ��ͼ�ס����dz�ǿ��ͬ��Բ�Ρ���������ǿ�ų�����Բ��ֱ���������α߳���ͬ����������������ͬ������������ͬ�ٶ��ش�ֱ�ڴų�������������ų�������Բ�δų������ӳ��ٶȷ����Բ�ģ����������δų������ӳ��ٶȷ���ֱ�ڱ߽��Ҵ��е���룬�����ӷֱ������ų���������ٶȱ仯��v������v���Ĵ�С��ϵΪ��������
��ͼ�ס����dz�ǿ��ͬ��Բ�Ρ���������ǿ�ų�����Բ��ֱ���������α߳���ͬ����������������ͬ������������ͬ�ٶ��ش�ֱ�ڴų�������������ų�������Բ�δų������ӳ��ٶȷ����Բ�ģ����������δų������ӳ��ٶȷ���ֱ�ڱ߽��Ҵ��е���룬�����ӷֱ������ų���������ٶȱ仯��v������v���Ĵ�С��ϵΪ��������| A�� | ��v������v�� | B�� | ��v������v�� | C�� | ��v���ܡ�v�� | D�� | ��v���ݡ�v�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
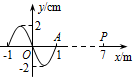 һ�����Ҵ����ļ�г����t=1sʱ�̵IJ�����ͼ��ʾ���پ���0.7s��x=7m�����ʵ�P��һ�δ�ƽ��λ����������ʱO���ʵ㴦��ƽ��λ�ã�ѡ����塱�������ȡ�����ƽ��λ�á��������в�������T=0.2s��
һ�����Ҵ����ļ�г����t=1sʱ�̵IJ�����ͼ��ʾ���پ���0.7s��x=7m�����ʵ�P��һ�δ�ƽ��λ����������ʱO���ʵ㴦��ƽ��λ�ã�ѡ����塱�������ȡ�����ƽ��λ�á��������в�������T=0.2s���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���ﴫ���� | B�� | ���崫���� | C�� | �¶ȴ����� | D�� | ѹ�������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
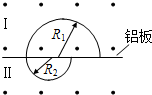 �����彫ͬһ��ǿ�ų��ֳɢ����������ٴ������ӿɴ�������һ�Σ������������˶��Ĺ켣��ͼ���뾶R1��R2���ٶ���������ǰ�����ӵ������ֲ��䣬������ӣ�������
�����彫ͬһ��ǿ�ų��ֳɢ����������ٴ������ӿɴ�������һ�Σ������������˶��Ĺ켣��ͼ���뾶R1��R2���ٶ���������ǰ�����ӵ������ֲ��䣬������ӣ�������| A�� | ������ | B�� | �ڢ�������˶��ٶ���ͬ | ||
| C�� | �ڢ�������˶�ʱ����ͬ | D�� | ������������˶�������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
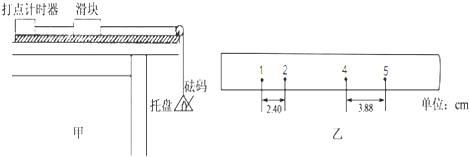
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���������������ٶ� | B�� | ��������ǵ����� | ||
| C�� | �������������е��ٶ� | D�� | �������������еļ��ٶ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com