
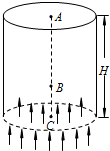
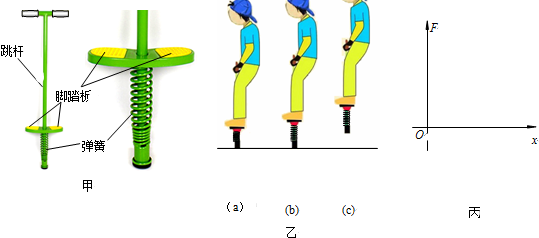
 “娱乐风洞”是一项将科技与惊险相结合的娱乐项目,它能在一个特定的空间内把表演者“吹”起来.假设风洞内向上的风量和风速保持不变,表演者调整身体的姿态,通过改变受风面积(表演者在垂直风力方向的投影面积),来改变所受向上风力的大小.已知人体所受风力大小与受风面积成正比,人水平横躺时受风面积最大,设为S0,站立时受风面积为$\frac{1}{8}$S0;当受风面积为$\frac{1}{2}$S0时,表演者恰好可以静止或匀速漂移.如图所示,某次表演中,人体可上下移动的空间总高度为H,表演者由静止以站立身姿从A位置下落,经过B位置时调整为水平横躺身姿(不计调整过程的时间和速度变化),运动到C位置速度恰好减为零.关于表演者下落的过程,下列说法中正确的是( )
“娱乐风洞”是一项将科技与惊险相结合的娱乐项目,它能在一个特定的空间内把表演者“吹”起来.假设风洞内向上的风量和风速保持不变,表演者调整身体的姿态,通过改变受风面积(表演者在垂直风力方向的投影面积),来改变所受向上风力的大小.已知人体所受风力大小与受风面积成正比,人水平横躺时受风面积最大,设为S0,站立时受风面积为$\frac{1}{8}$S0;当受风面积为$\frac{1}{2}$S0时,表演者恰好可以静止或匀速漂移.如图所示,某次表演中,人体可上下移动的空间总高度为H,表演者由静止以站立身姿从A位置下落,经过B位置时调整为水平横躺身姿(不计调整过程的时间和速度变化),运动到C位置速度恰好减为零.关于表演者下落的过程,下列说法中正确的是( )| A. | 从A至B过程表演者的加速度大于从B至C过程表演者的加速度 | |
| B. | 从A至B过程表演者的运动时间小于从B至C过程表演者的运动时间 | |
| C. | 从A至B过程表演者动能的变化量大于从B至C过程表演者克服风力所做的功 | |
| D. | 从A至B过程表演者动量变化量的数值小于从B至C过程表演者受风力冲量的数值 |
分析 加速度的关系根据牛顿第二定律分析.结合运动学公式分析运动时间关系.对两个过程分别动能定理列式,分析从A至B过程表演者动能的变化量从B 至C过程表演者克服风力所做的功的大小关系.由动量定理分析冲量关系.
解答 解:A、设人水平横躺时受到的风力大小为Fm,由于人体受风力大小与正对面积成正比,故人站立时风力为$\frac{1}{8}$Fm.
由于受风力有效面积是最大值的一半时,恰好可以静止或匀速漂移,故可以求得人的重力 G=$\frac{1}{2}$Fm,即有 Fm=2G.
则从A至B过程表演者的加速度为 a1=$\frac{G-\frac{1}{8}{F}_{m}}{m}$=$\frac{mg-\frac{1}{8}×2×mg}{m}$=0.75g
从B至C过程表演者的加速度大小为 a2=$\frac{{F}_{m}-G}{m}$=$\frac{2mg-mg}{m}$=g,因此从A至B过程表演者的加速度小于从B至C过程表演者的加速度.故A错误;
B、设B点的速度为v,则从A至B过程表演者的运动时间 t1=$\frac{v}{{a}_{1}}$=$\frac{4v}{3g}$.从B至C过程表演者的运动时间 t2=$\frac{v}{{a}_{2}}$=$\frac{v}{g}$,则t1>t2,故B错误.
C、由速度位移公式得:
从A至B过程表演者的位移 x1=$\frac{{v}^{2}}{2{a}_{1}}$,从B至C过程表演者的位移 x2=$\frac{{v}^{2}}{2{a}_{2}}$,故x1:x2=4:3
因而有 x1=$\frac{4}{7}$H
对A至B过程应用动能定理:表演者A至B动能的增量△Ek=(G-$\frac{1}{8}$Fm)•$\frac{4}{7}$H=$\frac{3}{7}$FmH
B至C克服风力做的功 W2=Fm•$\frac{3}{7}$H=$\frac{3}{7}$FmH
可知,△Ek=W2,即表演者A至B动能的增量等于B至C克服风力做的功,故C错误;
D、根据动量定理得:从A至B过程表演者动量变化量△p1=(G-$\frac{1}{8}$Fm)•t1=($\frac{1}{2}$Fm-$\frac{1}{8}$Fm)•$\frac{4v}{3g}$=$\frac{{F}_{m}v}{2g}$
从B至C过程表演者受风力冲量的数值 I2=Fm•t2=$\frac{{F}_{m}v}{g}$,则△p1<I2,即从A至B过程表演者动量变化量的数值小于从B至C过程表演者受风力冲量的数值.故D正确.
故选:D
点评 本题关键将下降过程分为匀加速过程和匀减速过程,求出各个过程的加速度,然后根据运动学公式列式判断.要知道动能关系可根据动能定理研究.冲量和动量关系可根据动量定理研究.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中物理 来源: 题型:选择题
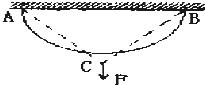 质量为m的绳子两端分别系在天花板上的A、B两点,A、B间距离小于绳长,整条绳悬垂情况如图实线所示.今在绳的中点C施加竖直向下的力,将绳子拉至如图虚线情况,则整条绳的重力势能( )
质量为m的绳子两端分别系在天花板上的A、B两点,A、B间距离小于绳长,整条绳悬垂情况如图实线所示.今在绳的中点C施加竖直向下的力,将绳子拉至如图虚线情况,则整条绳的重力势能( )| A. | 增大 | B. | 不变 | C. | 减小 | D. | 不确定 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
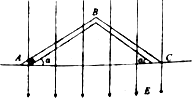 如图所示,一个“V”形玻璃管ABC倒置于平面内,并处于场强大小为E=1×103V/m,方向竖直向下的匀强电场中,一个重力为G=1×10-3N,电荷量为q=2×10-4C的带负电小滑块从A点由静止开始运动,小滑块与管壁的动摩擦因数μ=0.5.已知管长AB=BC=L=2m,倾角α=37°,B点是一段很短的光滑圆弧管,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法中正确的是( )
如图所示,一个“V”形玻璃管ABC倒置于平面内,并处于场强大小为E=1×103V/m,方向竖直向下的匀强电场中,一个重力为G=1×10-3N,电荷量为q=2×10-4C的带负电小滑块从A点由静止开始运动,小滑块与管壁的动摩擦因数μ=0.5.已知管长AB=BC=L=2m,倾角α=37°,B点是一段很短的光滑圆弧管,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法中正确的是( )| A. | B、A两点间的电势差为2000V | |
| B. | 小滑块从A点第一次运动到B点的过程中电势能增大 | |
| C. | 小滑块第一次速度为零的位置在C处 | |
| D. | 从开始运动到最后静止,小滑块通过的总路程为3m |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
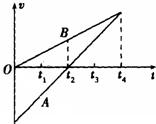 在一条宽马路上有A、B两车,在t=0时刻,两车刚好处于同一地点,接下来它们运动图象如图所示,那么,在0~t4时间内的情景是( )
在一条宽马路上有A、B两车,在t=0时刻,两车刚好处于同一地点,接下来它们运动图象如图所示,那么,在0~t4时间内的情景是( )| A. | A车在0~t2时间内做匀加速直线运动,在t2时刻改变运动方向 | |
| B. | 在t2时刻A车速度为零,然后反向运动,此时两车相距最远 | |
| C. | 在t4时刻,A车追上B车 | |
| D. | 在t4时刻,两车相距最远 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
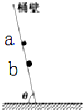 “飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶面上做圆周运动而不掉下来.如图所示为剖面图,已知桶壁的倾角为θ,两个演员的车和人的总质量为ma、mb,且ma>mb.若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )
“飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶面上做圆周运动而不掉下来.如图所示为剖面图,已知桶壁的倾角为θ,两个演员的车和人的总质量为ma、mb,且ma>mb.若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )| A. | 二者的速度相同 | B. | a处于高处,a的速度更大一些 | ||
| C. | 桶面对a和b支持力是一样的 | D. | a和b的加速度大小是一样的 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
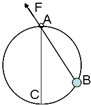 如图所示,竖直放置的半径为R的光滑圆环,AC为竖直方向的一条直径,A点有一光滑小孔,有一小环B套在圆环上,用一细线栓在小环B上,细线穿过小孔A,用拉力F拉小环B,使它沿圆周缓慢向上移动,在向上移动的过程中,关于拉力F与圆环对小环的弹力FN的说法正确的是( )
如图所示,竖直放置的半径为R的光滑圆环,AC为竖直方向的一条直径,A点有一光滑小孔,有一小环B套在圆环上,用一细线栓在小环B上,细线穿过小孔A,用拉力F拉小环B,使它沿圆周缓慢向上移动,在向上移动的过程中,关于拉力F与圆环对小环的弹力FN的说法正确的是( )| A. | FN的大小不变 | B. | FN大小一直变小 | C. | F先变小后变大 | D. | F一直变小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com