
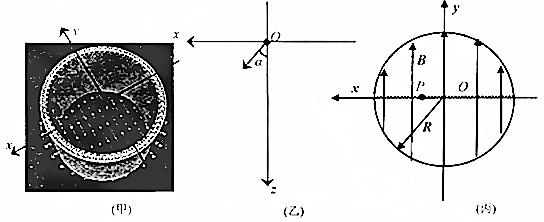
分析 (1)根据左手定则判断反电子所受洛伦兹力方向;
(2)反电子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,由几何关系得到半径满足的条件,即反电子的可求出速率;
(3)根据题意求出粒子运动轨道半径,粒子在磁场中做匀速圆周运动洛伦兹力提供向心力,由牛顿第二定律可以求出v以及b、s与v0之间的关系.
解答 解:(1)根据左手定则判断:反电子所受洛伦兹力方向:沿x轴负方向;
(2)反电子在匀强磁场中做匀速圆周运动洛伦兹力提供向心力,
由牛顿第二定律得:$evB=m\frac{{v}_{\;}^{2}}{r}$,
由几何关系得:R≤r+rcosα,
解得:$v≥\frac{eBR}{m(1+cosα)}$;
(3)当b≤s时,由几何关系:${r}_{\;}^{2}={s}_{\;}^{2}+(r-b)_{\;}^{2}$
解得:$r=\frac{{s}_{\;}^{2}+{b}_{\;}^{2}}{2b}$,
要求粒子垂直于筒壁方向速度大于已知速度${v}_{0}^{\;}$
即:$vcosα>{v}_{0}^{\;}$,
又因为:$cosα=\frac{s}{r}=\frac{2bs}{{b}_{\;}^{2}+{s}_{\;}^{2}}$
所以$\frac{2bsv}{{b}_{\;}^{2}+{s}_{\;}^{2}}>{v}_{0}^{\;}$
当b>s时,由几何关系:${r}_{\;}^{2}={s}_{\;}^{2}+(b-r)_{\;}^{2}$
所以:$r=\frac{{s}_{\;}^{2}+{b}_{\;}^{2}}{2b}$
要求粒子垂直于筒壁方向速度大于已知速度${v}_{0}^{\;}$
即:$vcosα>{v}_{0}^{\;}$
又因为:$cosα=\frac{s}{r}=\frac{2bs}{{b}_{\;}^{2}+{s}_{\;}^{2}}$
所以:$\frac{2bsv}{{b}_{\;}^{2}+{s}_{\;}^{2}}>{v}_{0}^{\;}$,
当b=s时,则r=b=s,$v>{v}_{0}^{\;}$;
答:(1)若反电子垂直于xoy平面从O点打入桶中,反电子所受洛仑兹力的方向:沿x轴负方向;
(2)要使反电子能打在桶壁,则反电子的速率为:$v≥\frac{eBR}{m(1+cosα)}$;
(3)入射速度v以及b、s与v0之间应满足什么关系为:①当b≤s时,$\frac{2bsv}{{b}_{\;}^{2}+{s}_{\;}^{2}}>{v}_{0}^{\;}$;②当b>s时,$\frac{2bsv}{{b}_{\;}^{2}+{s}_{\;}^{2}}>{v}_{0}^{\;}$;③当b=s时,$v>{v}_{0}^{\;}$.
点评 本题考查了粒子在磁场中的运动,认真审题理解题意、分析清楚粒子运动过程是解题的前提与关键,应用左手定则、知道洛伦兹力提供向心力应用牛顿第二定律可以解题;要掌握处理带电粒子在磁场中运动的方法.


科目:高中物理 来源: 题型:选择题
 如图所示,框架面积为S,框架平面与磁感应强度为B的匀强磁场方向垂直,则下列穿过平面的磁通量的说法中不正确的是( )
如图所示,框架面积为S,框架平面与磁感应强度为B的匀强磁场方向垂直,则下列穿过平面的磁通量的说法中不正确的是( )| A. | 如图所示位置时等于BS | |
| B. | 若使框架绕OO′转过60°角,磁通量为$\frac{1}{2}$BS | |
| C. | 若从初始位置转过90°角,磁通量为BS | |
| D. | 若从初始位置转过180°角,磁通量变化为2BS |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图甲为倾角θ=30°的绝缘光滑匀质直角斜面体,其直角棱固定在水平地面上的光滑转动轴上,斜面长l=2m.斜面体顶端固定一个半径r=$\sqrt{3}$m的轻质绝缘光滑圆弧轨道,圆弧轨道和斜面体底边中点在同一竖直平面内,斜面体与圆弧轨道平滑连接,圆弧轨道顶端的切线方向恰好竖直.其正视图如图乙所示.圆弧轨道所在的空间区域有竖直向上的匀强电场,场强大小E=1.0×103V/m,圆弧轨道上方和下方均无电场.一个带电量q=+1.0×10-3C、质量m=0.1kg的小球(可视为质点)从斜面体底边中点处以初速度v0=$\sqrt{22}$m/s垂直底边沿斜面向上滑动,斜面体始终处于静止状态,不计空气阻力,g=10m/s2.试求:
如图甲为倾角θ=30°的绝缘光滑匀质直角斜面体,其直角棱固定在水平地面上的光滑转动轴上,斜面长l=2m.斜面体顶端固定一个半径r=$\sqrt{3}$m的轻质绝缘光滑圆弧轨道,圆弧轨道和斜面体底边中点在同一竖直平面内,斜面体与圆弧轨道平滑连接,圆弧轨道顶端的切线方向恰好竖直.其正视图如图乙所示.圆弧轨道所在的空间区域有竖直向上的匀强电场,场强大小E=1.0×103V/m,圆弧轨道上方和下方均无电场.一个带电量q=+1.0×10-3C、质量m=0.1kg的小球(可视为质点)从斜面体底边中点处以初速度v0=$\sqrt{22}$m/s垂直底边沿斜面向上滑动,斜面体始终处于静止状态,不计空气阻力,g=10m/s2.试求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
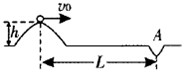 随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面的坡上水平击出一个质量为的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为的A洞.则( )
随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面的坡上水平击出一个质量为的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为的A洞.则( )| A. | 球被击出后做平抛运动 | |
| B. | 该球从被击出到落入A洞所用的时间为$\sqrt{\frac{2h}{g}}$ | |
| C. | 球被击出时的初速度大小为L$\sqrt{\frac{g}{2h}}$ | |
| D. | 球被击出后受到的水平风力的大小$\frac{mgh}{L}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在如图所示的电路中,线圈中的自感系数很大,且其直流电阻可以忽略不计.D1和D2是两个完全相同的小灯泡,在开关S的闭合和断开的过程中(灯丝不会断),D1和D2亮度的变化情况是( )
在如图所示的电路中,线圈中的自感系数很大,且其直流电阻可以忽略不计.D1和D2是两个完全相同的小灯泡,在开关S的闭合和断开的过程中(灯丝不会断),D1和D2亮度的变化情况是( )| A. | S闭合,D1很亮且亮度不变,D2逐渐变亮,最后两灯一样亮;S断开,D2立即灭,D1逐渐变亮 | |
| B. | S闭合,D1不亮,D2很亮;S断开,D2立即灭 | |
| C. | S闭合,D1和D2同时亮,而后D1灭,D2亮度不变:S断开,D2立即灭,D1亮一下才灭 | |
| D. | S闭合,D1和D2同时亮,后D1逐渐熄灭,D2则逐渐变得更亮;S断开,D2立即灭,D1亮一下后才灭 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com