
分析 同步卫星总是在赤道上空,其高度也是一定的.由它画一条到地球表面的切线,可见两极周围的区域内就收不到微波通讯.
根据万有引力提供向心力和数学几何关系求解.根据几何关系求出极地卫星的轨道半径,由万有引力提供向心力即可求出极地卫星的周期.
解答  解:以m、M分别表示同步卫星和地球的质量,r表示同步卫星到地心的距离,T表示地球的自转周期,则
解:以m、M分别表示同步卫星和地球的质量,r表示同步卫星到地心的距离,T表示地球的自转周期,则
$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$
地球表面万有引力等于重力$G\frac{Mm}{{R}_{0}^{2}}=mg$
根据几何关系:$rsinα={R}_{0}^{\;}$
对于极地卫星,轨道半径为r′,周期为T′
$r′cosα={R}_{0}^{\;}$
有$G\frac{Mm}{r{′}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{T{′}_{\;}^{2}}r′$
得$T′=\sqrt{\frac{r{′}_{\;}^{3}}{{r}_{\;}^{3}}}T$=$(\frac{{R}_{0}^{\;}}{\sqrt{(\frac{g{R}_{0}^{2}{T}_{\;}^{2}}{4{π}_{\;}^{2}})}-{R}_{0}^{2}})^{\frac{3}{2}}T$
答:这颗极地卫星绕地球的周期至少为$(\frac{{R}_{0}^{\;}}{\sqrt{(\frac{g{R}_{0}^{2}{T}_{\;}^{2}}{4{π}_{\;}^{2}})}-{R}_{0}^{2}})^{\frac{3}{2}}T$
点评 解决该题关键要根据题意找出收不到微波区域的面积,善于把物理问题与数学几何图形结合运用


 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
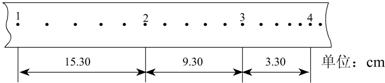
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | UI | B. | UI-I2R | C. | UI+I2R | D. | $\frac{{U}^{2}}{R}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | M=$\frac{{4{π^2}{{(R+h)}^3}}}{{G{T^2}}}$ | B. | M=$\frac{(R+h)^{2}g}{G}$ | C. | M=$\frac{{4{π^2}{R^3}}}{{G{T^2}}}$ | D. | M=$\frac{4{π}^{2}{h}^{3}}{G{T}^{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
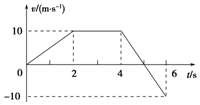 一物体自t=0时开始做直线运动,其速度图线如图所示,求:
一物体自t=0时开始做直线运动,其速度图线如图所示,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 电势ΦA<ΦB,场强EA<EB | |
| B. | 电势ΦA>ΦB,场强EA>EB | |
| C. | 将+q电荷从A点移动到B点电场力做正功 | |
| D. | 将-q电荷分别放在A、B两点时具有的电势能EPA>EPB |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
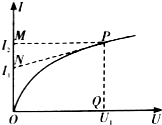 某电子元件通电后其电流I随所加电压U变化的图线如图所示,P为图线上一点,PN为图线的切线,PQ为U轴的垂线,PM为I轴的垂线,下列说法中正确的是( )
某电子元件通电后其电流I随所加电压U变化的图线如图所示,P为图线上一点,PN为图线的切线,PQ为U轴的垂线,PM为I轴的垂线,下列说法中正确的是( )| A. | 随着所加电压的增大,该元件的电阻增大 | |
| B. | 对应P点,该元件的电阻为R=$\frac{{U}_{1}}{{I}_{1}}$ | |
| C. | 对应P点,该元件的电阻为R=$\frac{{U}_{1}}{{I}_{2}-{I}_{1}}$ | |
| D. | 该元件为非线性元件 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 该定义只适用于点电荷产生的电场 | |
| B. | 库仑定律的表达式F=k$\frac{{q}_{1}{q}_{2}}{{r}^{2}}$可以说是点电荷q2产生的电场在点电荷q1处的库仑力大小;而k$\frac{{q}_{1}}{{r}^{2}}$可以说是点电荷q2产生的电场在点电荷q1处的场强大小 | |
| C. | 对E=$\frac{F}{q}$,F是放入电场中的点电荷所受的静电力,q是产生电场的电荷的电荷量 | |
| D. | 电场中某点场强的方向与试探电荷的正负无关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com