
 ��ͼ��ʾ������д��ڿռ䷶Χ�㹻����ˮƽ���ҵ���ǿ�ų����ڵ糡�У�һ������Ϊm�������Ϊq�����ӣ��Դ�СΪV0�ij��ٶȴ�O������糡������ɦ�=45��ǵķ���������ֱ���˶���
��ͼ��ʾ������д��ڿռ䷶Χ�㹻����ˮƽ���ҵ���ǿ�ų����ڵ糡�У�һ������Ϊm�������Ϊq�����ӣ��Դ�СΪV0�ij��ٶȴ�O������糡������ɦ�=45��ǵķ���������ֱ���˶������� ��1�����������������糡�������ö���ֱ���˶����������������ĺ���һ�����˶������ֱ���ϣ��������ĺϳɿ���õ糡������ţ�ٵڶ����ɿ���ü��ٶȣ���λ�ƹ�ʽ���λ�ƣ������ɹ��Ĺ�ʽ��õ糡���Ĺ���
��2�����糡������������������˶���������ֱ����ֻ����������ˮƽ����ֻ�ܵ糡���������˶�ѧ��ʽ���ʱ�䣬��ŷλ��ʱ�乫ʽ����ڵ糡��������ͨ����λ�Ƽ�����õ糡��������
��� �⣺��1����С��ĵ����Ϊq����С����ֱ���˶��������ܵ��ľ�����Eq������mg�ĺ������������ٶȷ�����ͬһֱ����
��mg=qE
С�����ȼ����˶��ļ��ٶȴ�СΪ��
a=$\frac{F}{m}=\frac{\sqrt{2}mg}{m}=\sqrt{2}g$��
��ˮƽ�������ֱ����ļ��ٶ�Ϊax=ay=g
�ٶȼ�Ϊ��ͨ����λ��ΪX=$\frac{{v}_{0}^{2}}{2a}=\frac{{v}_{0}^{2}}{2\sqrt{2}g}$
ˮƽ����ͨ����λ��Ϊx=Xcos45��=$\frac{{v}_{0}^{2}}{4g}$
���Ʋ�ΪU=mgx=$\frac{{mv}_{0}^{2}}{4}$
����ʱ��Ϊt=$\frac{{v}_{0}}{\sqrt{2}g}$
��2��������ˮƽ�������ֱ����ķ��ٶ�Ϊ${v}_{0x}={v}_{0y}=\frac{\sqrt{2}}{2}{v}_{0}$
���ٶȼ�Ϊ$\frac{1}{2}{v}_{0}$ʱ����ʱ����ˮƽ�������ֱ����ķ��ٶ�Ϊ${v��}_{0x}={v��}_{0y}=\frac{\sqrt{2}}{4}{v}_{0}$
������ʱ��Ϊ$t��=\frac{\sqrt{2}{v}_{0}}{4g}$
���糡�������ʱ��t���ٶȴﵽv0����v��x=v��0x+gt��
v��y=v��0y-gt��
${v}_{0}=\sqrt{��v{��}_{x}��^{2}+��v{��}_{y}��^{2}}$
�������t��=$\frac{\sqrt{6}{v}_{0}}{4g}$
��ʱ��t�����ص糡����ͨ����λ��Ϊ$x��=v{��}_{0x}t��+\frac{1}{2}{a}_{y}t{��}^{2}=\frac{{\sqrt{3}v}_{0}^{2}}{2g}+\frac{{3v}_{0}^{2}}{16g}$
�糡������ΪW=mgx$��=mg��\frac{{\sqrt{3}v}_{0}^{2}}{2g}+\frac{{3v}_{0}^{2}}{16g}��$
�𣺣�1���������˶�����ߵ��������֮��ĵ��Ʋ�$\frac{{mv}_{0}^{2}}{4}$�������˶�����ߵ����õ�ʱ��$\frac{\sqrt{2}{v}_{0}}{4g}$
��2���������˶����ٶȴ�СΪ$\frac{1}{2}$V0ʱ���������糡�ķ�����С���ֲ��䣬�����ӵ��ٶȴ�С�ٴα�ΪV0ʱ�����������Ϊ$mg��\frac{{\sqrt{3}v}_{0}^{2}}{2g}+\frac{{3v}_{0}^{2}}{16g}��$
���� ������Ҫ�����������������͵糡�������µ�ֱ���˶��������˶����������˶������л�������˶��ֽ�Ϊֱ���˶�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ������ΪL���㹻����ƽ�н�������̶��ھ�Եˮƽ���ϣ����������������ֵR�ĵ��裮�������ڿռ������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��ΪB��һ������m�ĵ����MN���ڵ������뵼��Ӵ����ã����������Ч����ҲΪR��������뵼���Ķ�Ħ������Ϊ�̣������Ħ�������ڻ���Ħ�����������MN�ij�ʼλ���뵼������˾���ΪL������ĵ���ɺ��Բ��ƣ�
��ͼ��ʾ������ΪL���㹻����ƽ�н�������̶��ھ�Եˮƽ���ϣ����������������ֵR�ĵ��裮�������ڿռ������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��ΪB��һ������m�ĵ����MN���ڵ������뵼��Ӵ����ã����������Ч����ҲΪR��������뵼���Ķ�Ħ������Ϊ�̣������Ħ�������ڻ���Ħ�����������MN�ij�ʼλ���뵼������˾���ΪL������ĵ���ɺ��Բ��ƣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ӡ�������ǵ�������һ�������Ľ����������ý��ڳ���ϣ���ij������������ڳ���Ͽշ��У����ǵĹ��ƽ����������غϣ���֪���ǹ���뾶Ϊr�����з�����������ת������ͬ���������ת���ٶ�Ϊ��0������뾶ΪR����������������ٶ�Ϊg��������ijʱ��ͨ����һ����������Ϸ�����������ٴξ������λ����Ҫ�����ʱ��Ϊ��������
��ӡ�������ǵ�������һ�������Ľ����������ý��ڳ���ϣ���ij������������ڳ���Ͽշ��У����ǵĹ��ƽ����������غϣ���֪���ǹ���뾶Ϊr�����з�����������ת������ͬ���������ת���ٶ�Ϊ��0������뾶ΪR����������������ٶ�Ϊg��������ijʱ��ͨ����һ����������Ϸ�����������ٴξ������λ����Ҫ�����ʱ��Ϊ��������| A�� | $\frac{2��}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | B�� | $\frac{2��}{{��}_{0}+\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | C�� | $\frac{2��}{{��}_{0}-\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | D�� | $\frac{2��}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}-{��}_{0}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
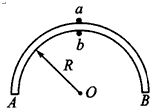 ��ͼ��ʾ��ABΪ�뾶ΪR�Ľ������죬a��bΪ�ֱ��ص���������������Բ���˶���С��ҪʹС�������뵼�죬��a��b�ڵ�����ߵ���ٶ�va��vbӦ����ʲô������
��ͼ��ʾ��ABΪ�뾶ΪR�Ľ������죬a��bΪ�ֱ��ص���������������Բ���˶���С��ҪʹС�������뵼�죬��a��b�ڵ�����ߵ���ٶ�va��vbӦ����ʲô�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
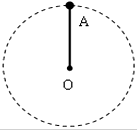 ��ͼ��ʾ����L=0.5m�������ɺ��Ե�ϸ������һ�˹̶���O�㣬�϶�������һ���������A��A������Ϊ1kg������O������ֱƽ������Բ���˶���ȡ�������ٶ�g=10m/s2�������Aͨ����ߵ�ʱ������������⣺
��ͼ��ʾ����L=0.5m�������ɺ��Ե�ϸ������һ�˹̶���O�㣬�϶�������һ���������A��A������Ϊ1kg������O������ֱƽ������Բ���˶���ȡ�������ٶ�g=10m/s2�������Aͨ����ߵ�ʱ������������⣺�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ����ͨ�����⾵�ֽ�Ϊ�ɺ쵽�ϰ�˳�����еIJ�ɫ��������ף�����������������ɫɢ����ԭ�������ڲ����Ը���ɫ��������ʲ�ͬ������ͼ���ǿ��Եõ���
��ͼ��ʾ����ͨ�����⾵�ֽ�Ϊ�ɺ쵽�ϰ�˳�����еIJ�ɫ��������ף�����������������ɫɢ����ԭ�������ڲ����Ը���ɫ��������ʲ�ͬ������ͼ���ǿ��Եõ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ����г�˶�������ÿ��ͨ��ͬһλ��ʱ��������ͬ�ļ��ٶȺ��ٶ� | |
| B�� | �Შ�ڴ��������У������ϵ��ʵ��˶������ڵIJ������õ�ʱ��Ϊһ������ | |
| C�� | һ�����ɽ���б��������������Ͽ���ֻ�������������û���������� | |
| D�� | ˮ����Ĥ���ֲ�ɫ�����ǹ�ĸ���������˵���˹���һ�ֲ� | |
| E�� | �ڵ糡��Χһ�����ڴų����ڴų���Χһ�����ڵ糡 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
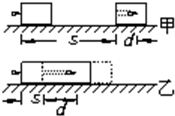 ľ������Ϊd��Ϊ��ʾ�ù��̣��ס�����ͬѧ�ֱ�����ͼ��ʾ��ʾ��ͼ�����ӵ�����ľ���ʱ�伫�̣����ڼס�����ͼ�ķ���������˵������ȷ���� ��������
ľ������Ϊd��Ϊ��ʾ�ù��̣��ס�����ͬѧ�ֱ�����ͼ��ʾ��ʾ��ͼ�����ӵ�����ľ���ʱ�伫�̣����ڼס�����ͼ�ķ���������˵������ȷ���� ��������| A�� | ��ˮƽ��⻬ʱ��ͼ��ȷ����ˮƽ��ֲ�ʱ��ͼ��ȷ | |
| B�� | ���ӵ��ٶȽϴ�ʱ��ͼ��ȷ�����ӵ��ٶȽ�Сʱ��ͼ��ȷ | |
| C�� | ��ˮƽ��⻬����M��mʱ����ͼ��ȷ����M��mʱ��ͼ��ȷ | |
| D�� | ����ˮƽ���Ƿ�⻬���ٶȡ�������С��ϵ��Σ�������ͼ��ȷ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com