
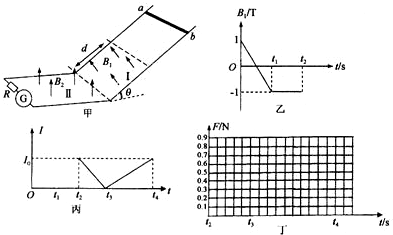
分析 (1)题中电流表的示数保持不变,整个下滑过程中回路中产生的感应电动势不变,可判断出在t1时刻棒刚好进入磁场Ⅰ区域且做匀速直线运动,由平衡条件和安培力、欧姆定律、法拉第定律结合求解v;
(2)棒没进入磁场以前做匀加速直线运动,由牛顿第二定律和运动学公式求出下滑的距离,由于棒进入磁场后产生的感应电动势不变,由法拉第电磁感应定律求出磁场区I在沿斜轨方向上的宽度d;
(3)ab棒进入磁场以前,由焦耳定律求出ab棒产生的焦耳热.进入磁场Ⅰ的过程中,棒的重力势能减小转化为内能,由能量守恒求出ab棒产生的焦耳热;
(4)根据图线写出I-t′方程式,由欧姆定律I=$\frac{E}{R+r}$=$\frac{BLv}{R+r}$,得到速度与时间的表达式,即可求出加速度,由牛顿第二定律得到外力F与时间t的关系式,作出图象.
解答 解:(1)电流表的示数不变,说明在整个下滑过程中回路的电动势是不变的,说明在B变化时和不变时感应电动势大小一样,所以可以判断在t1时刻棒刚好进入磁场区域且做匀速直线运动.
由平衡条件有:mgsinθ-BIL=0
由欧姆定律有:$I=\frac{{E}_{1}}{R+r}$,E1=BLv,
代入数值得:v=2.5m/s
(2)棒没进入磁场以前做匀加速直线运动,加速度是:a=gsin30°=5m/s2,
棒刚磁场时的速度 v=at1,
得:t1=$\frac{v}{a}$=$\frac{2.5}{5}s$=0.5s
下滑的距离是:s1=$\frac{1}{2}$at12=$\frac{1}{2}×5×0.{5}^{2}m$=0.625m
在棒没进入磁场以前,由于B1均匀变化,所以有:E2=$\frac{△B}{△t}Ld$,
又 E1=B1Lv,E1=E2,
代入得 4×1×d=1×1×2.5,
解得:d=0.625m
(3)ab棒进入磁场以前,棒上产生的热量为:Q1=I2Rt1=0.52×2×0.5J=0.25J
取ab棒在斜轨磁场中运动为研究过程,有:mgdsinθ-Q2=0
得:Q2=0.3125J.
此时,棒上产生的热量是:Q2r=$\frac{r}{r+R}{Q}_{2}$=$\frac{2}{2+3}×0.3125J$=0.125J
则棒上产生的总热量是:Qr=Q1+Q2r=0.25J+0.125J=0.375 J
或:Qr=I2R(t1+t2)=0.52×2×(0.5+0.25)J=0.375J
(4)因为E=BLv,所以刚进水平轨道时时的电动势是:E=2.5V,I0=$\frac{E}{R+r}=\frac{2.5}{3+2}A$=0.5A
取t2时刻为零时刻,则根据图线可以写出I-t的方程式:I=0.5-tˊ,I=$\frac{BLv}{R+r}$,
则v=2.5-5 tˊ,所以a1=5m/s2.
由牛顿第二定律可得:F+B2IL=ma1,F+I=1
F=tˊ,画在坐标系里.
由丙图可以同理得出棒运动的加速度大小是:a2=2.5m/s2,
依据牛顿定律得:F-BIL=ma2
取t3时刻为零时刻,可以写出t3时刻后的I与时间的关系式,I=0.5 t,代入上面的式子可以得到F=0.25+0.5t,画在坐标系里.
答:(1)ab棒进入磁场区I时速度V的大小是2.5m/s;
(2)磁场区I在沿斜轨方向上的宽度d是0.625m;
(3)棒从开始运动到刚好进入水平轨道这段时间内ab棒上产生的热量Q是0.375J;
(4)作出t2到t4时间内外力大小F随时间t变化的函数图象如图所示.
点评 本题关键要正确分析导体棒的运动情况,判断其受力情况,运用法拉第定律、欧姆定律、焦耳定律及力学中牛顿第二定律等等多个知识解答,综合性很强,同时,考查了运用数学知识处理物理问题的能力.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:选择题

| A. | 20s末甲、乙两物体间相遇 | |
| B. | 前40s内甲、乙两物体间的距离逐渐减小,40s末乙追上甲 | |
| C. | 前40s内甲、乙两物体间距离一直在增大,40s末达到最大 | |
| D. | 前40s内甲、乙两物体间的距离先增大后减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 相对静止的物体间一定没有摩擦力 | |
| B. | 摩擦力的大小跟正压力成正比 | |
| C. | 滑动摩擦力的方向总是沿着接触面,并且跟物体的运动方向相反 | |
| D. | 静摩擦力的方向总是沿着接触面,可能跟物体的运动方向相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,水平地面上一辆质量M=4kg上表面光滑的平板小车长L=2m,上表面离地高h=0.8m,车运动时所受摩擦阻力为其重力的k倍,车上左侧有一挡板,紧靠挡板处有一可看成质点的小球,小球质量m=1kg.水平向右力F=10N作用在小车上,使小车与小球一起在水平面上向右做匀速直线运动,速度大小为v0=2m/s.t0时刻将水平向右力F改为水平向左,大小不变,经过一段时间后,小球从小车右端滑出并落到地面上.(假设滑动摩擦力近似等于最大静摩擦力)求:
如图所示,水平地面上一辆质量M=4kg上表面光滑的平板小车长L=2m,上表面离地高h=0.8m,车运动时所受摩擦阻力为其重力的k倍,车上左侧有一挡板,紧靠挡板处有一可看成质点的小球,小球质量m=1kg.水平向右力F=10N作用在小车上,使小车与小球一起在水平面上向右做匀速直线运动,速度大小为v0=2m/s.t0时刻将水平向右力F改为水平向左,大小不变,经过一段时间后,小球从小车右端滑出并落到地面上.(假设滑动摩擦力近似等于最大静摩擦力)求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
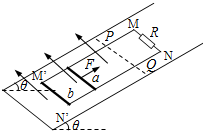 如图,两条平行的粗糙金属导轨MM′、NN′固定在倾角为θ=37°的绝缘斜面上,导轨间距d=0.5m,导轨上端连接一个定值电阻.导体棒a、b放在导轨上,与导轨垂直并良好接触.斜面上水平虚线PQ以下区域内,存在着垂直穿过斜面向上的匀强磁场,磁感应强度为B=2T.现对a棒施以平行导轨斜向上的拉力,使它沿导轨匀速向上运动,此时放在导轨下端的b棒处于静止并恰好不受摩擦力.当a棒运动到磁场的上边界PQ处时,撤去拉力,a棒将继续沿导轨向上运动一小段距离后再向下滑动,此时b棒已滑离导轨.当a棒再次滑回到磁场上边界PQ处时,又恰能沿导轨匀速向下运动.已知a棒的电阻r=1Ω,b棒和定值电阻的阻值均为R=2Ω,a棒的质量ma=0.2kg,b棒的质量mb=0.1kg,取重力加速度g=10m/s2,导轨电阻不计.求(sin37°=0.6,cos37°=0.8)
如图,两条平行的粗糙金属导轨MM′、NN′固定在倾角为θ=37°的绝缘斜面上,导轨间距d=0.5m,导轨上端连接一个定值电阻.导体棒a、b放在导轨上,与导轨垂直并良好接触.斜面上水平虚线PQ以下区域内,存在着垂直穿过斜面向上的匀强磁场,磁感应强度为B=2T.现对a棒施以平行导轨斜向上的拉力,使它沿导轨匀速向上运动,此时放在导轨下端的b棒处于静止并恰好不受摩擦力.当a棒运动到磁场的上边界PQ处时,撤去拉力,a棒将继续沿导轨向上运动一小段距离后再向下滑动,此时b棒已滑离导轨.当a棒再次滑回到磁场上边界PQ处时,又恰能沿导轨匀速向下运动.已知a棒的电阻r=1Ω,b棒和定值电阻的阻值均为R=2Ω,a棒的质量ma=0.2kg,b棒的质量mb=0.1kg,取重力加速度g=10m/s2,导轨电阻不计.求(sin37°=0.6,cos37°=0.8)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 一质量为m的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨与杆的电阻不计,金属杆向上滑行到某一高度之后又返回到底端,则在此全过程中( )
一质量为m的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨与杆的电阻不计,金属杆向上滑行到某一高度之后又返回到底端,则在此全过程中( )| A. | 向上滑行的时间大于向下滑行的时间 | |
| B. | 电阻R上产生的热量向上滑行时大于向下滑行时 | |
| C. | 通过电阻R的电量向上滑行时小于向下滑行时 | |
| D. | 杆a、b克服磁场力的功向上滑行时小于向下滑行时 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
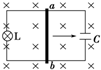 如图所示,匀强磁场的方向垂直于电路所在平面,导体棒ab与电路接触良好.当导体棒ab在外力F作用下从左向右做匀加速直线运动时,若不计摩擦和导线的电阻,整个过程中,灯泡L未被烧毁,电容器C未被击穿,则该过程中( )
如图所示,匀强磁场的方向垂直于电路所在平面,导体棒ab与电路接触良好.当导体棒ab在外力F作用下从左向右做匀加速直线运动时,若不计摩擦和导线的电阻,整个过程中,灯泡L未被烧毁,电容器C未被击穿,则该过程中( )| A. | 感应电动势将变大 | B. | 灯泡L的亮度变亮 | ||
| C. | 电容器C的上极板带负电 | D. | 电容器两极板间的电场强度将减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
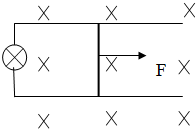 如图,轨道平面为水平面的光滑水平轨道,轨道间距d=0.5m.垂直于轨道平面的匀强磁场,磁感应强度B=0.8T.一电阻r=2Ω的导体杆AB与轨道保持良好接触,轨道左端皆有“6V3W”的灯泡.水平外力F作用于杆,使杆由静止开始运动,稳定后灯泡正常发光,试讨论:(金属导轨电阻不计)
如图,轨道平面为水平面的光滑水平轨道,轨道间距d=0.5m.垂直于轨道平面的匀强磁场,磁感应强度B=0.8T.一电阻r=2Ω的导体杆AB与轨道保持良好接触,轨道左端皆有“6V3W”的灯泡.水平外力F作用于杆,使杆由静止开始运动,稳定后灯泡正常发光,试讨论:(金属导轨电阻不计)查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | t2时刻是线框全部进入磁场瞬间,t4时刻是线框全部离开磁场瞬间 | |
| B. | 从bc边进入磁场起一直到ad边离开磁场为止,感应电流所做的功为mgs | |
| C. | v1的大小可能为$\frac{mgR}{{B}^{2}{L}^{2}}$ | |
| D. | 线框穿出磁场过程中流经线框横截面的电荷量比线框进入磁场过程中流经线框横截面的电荷量多 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com