
分析 由轨道能级表达式,得出跃迁时释放的能量,并根据动量与能量守恒定律,结合数学知识,同时由v0达到最小值v0min,此时vA=vB,即可求解.
解答 解:若两氢原子发生完全非弹性碰撞,则两原子碰撞后的速度相同,取开始时原子的运动方向为正方向,则:mv0=mv+mv
所以:v=$\frac{1}{2}{v}_{0}$
为使氢原子从基态跃迁到激发态,需要能量最小的激发态是n=2的第一激发态.已知氢原子的能量与其主量子数的平方成反比.${E}_{n}=\frac{{E}_{1}}{{n}^{2}}$…①
n=2的第一激发态的能量为${E}_{2}=\frac{{E}_{1}}{{2}^{2}}$…②
为使基态的氢原子激发到第一激发态所需能量为E内=E2-E1…③
这就是氢原子从第一激发态跃迁到基态时发出的光子的能量,即hν=E内…④
式中ν为光子的频率,从开始碰到发射出光子,根据动量和能量守恒定律有mv0=mvA+mvB+光子的动量…⑤
$\frac{1}{2}mv_0^2=\frac{1}{2}m(v_A^2+v_B^2)+hν$…⑥
光子的动量${p_ν}=\frac{hν}{c}$.由⑥式可推得$m{v_0}>\frac{2hν}{v_0}$,
因为v0<<c,所以$m{v_0}>>\frac{hν}{c}$,
故⑤式中光子的动量与mv0相比较可忽略不计,⑤式变为mv0=mvA+mvB=m(vA+vB)…⑦
符合⑥⑦两式的v0的最小值可推求如下:
由⑥式及⑦式可推得:
$\begin{array}{l}\frac{1}{2}mv_0^2=\frac{1}{2}m{(v_A^{\;}+v_B^{\;})^2}-m{v_A}{v_B}+hν\\ \;\;\;\;\;{\;}_{\;}=\frac{1}{2}mv_0^2-m{v_A}({v_0}-{v_A})+hν\end{array}$
且$mv_A^2-m{v_A}{v_0}+hν=0$
经配方得$m{({{v_A}-\frac{1}{2}{v_0}})^2}-\frac{1}{4}mv_0^2+hν=0$
$\frac{1}{4}mv_0^2=hν+m{({{v_A}-\frac{1}{2}{v_0}})^2}$…⑧
由(8)式可看出,当${v_A}=\frac{1}{2}{v_0}$时,v0达到最小值v0min,此时vA=vB…⑨
vomin=2$\sqrt{\frac{hγ}{m}}$…⑩
代入有关数据得:${v}_{0min}=\sqrt{\frac{-3{E}_{1}}{m}}$
故答案为:$\frac{v_0}{2},\sqrt{\frac{{-3{E_1}}}{m}}$
点评 考查轨道能级表达式的应用,注意动量与能量守恒定律的巧用,当心数学运算的正确性,同时掌握什么情况下,速度达到最小,是解题的关键.


科目:高中物理 来源: 题型:选择题
| A. | 水的饱和汽压随体积的升高而增大 | |
| B. | 扩散现象表明,分子在永不停息地运动 | |
| C. | 当分子间距离增大时,分子间引力增大,分子间斥力减小 | |
| D. | 一定质量的理想气体,在等压膨胀过程中,气体分子的平均动能减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
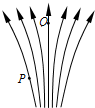
| A. | P点电势高于Q点电势 | |
| B. | P、Q两点场强大小相等、方向相同 | |
| C. | 同一正电荷分别置于P、Q两点时电势能相等 | |
| D. | 同一负电荷从P点移至Q点,电场力做负功,电势能增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
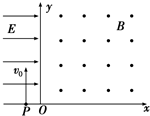 如图所示,在第二象限中有水平向右的匀强电场,电场强度为E,在第一象限内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.有一重力不计的带电粒子以垂直于x轴的速度v0=10m/s从x轴上的P点进入匀强电场,恰好与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入第四象限.已知OP之间的距离为d=0.5m,则带电粒子( )
如图所示,在第二象限中有水平向右的匀强电场,电场强度为E,在第一象限内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.有一重力不计的带电粒子以垂直于x轴的速度v0=10m/s从x轴上的P点进入匀强电场,恰好与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入第四象限.已知OP之间的距离为d=0.5m,则带电粒子( )| A. | 带正电荷 | B. | 在电场中运动的时间为0.1s | ||
| C. | 在磁场中做圆周运动的半径为$\frac{\sqrt{2}}{2}$m | D. | 在磁场中运动的时间为$\frac{3π}{40}$s |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
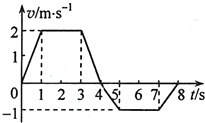 一质点沿x轴做直线运动,其V-t图象如图所示.质点在v=0时位于x=5m处,开始沿x轴正向运动.当t=8s时,质点在轴上的位置为( )
一质点沿x轴做直线运动,其V-t图象如图所示.质点在v=0时位于x=5m处,开始沿x轴正向运动.当t=8s时,质点在轴上的位置为( )| A. | x=3m | B. | x=8m | C. | x=9m | D. | x=-14m |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
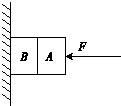 如图所示,初始时A、B两木块在水平方向的外力作用下挤压在竖直墙面上处于静止状态,A与B、B与墙面之间的动摩擦因数为μ=0.1,且最大静摩擦力等于滑动摩擦.两木块质量相等,都为1kg,当外力F变为下列不同值时,关于A、B之间的摩擦力f1,B与墙壁之间的摩擦力f2的大小,下列说法正确的是(g取10m/s2)( )
如图所示,初始时A、B两木块在水平方向的外力作用下挤压在竖直墙面上处于静止状态,A与B、B与墙面之间的动摩擦因数为μ=0.1,且最大静摩擦力等于滑动摩擦.两木块质量相等,都为1kg,当外力F变为下列不同值时,关于A、B之间的摩擦力f1,B与墙壁之间的摩擦力f2的大小,下列说法正确的是(g取10m/s2)( )| A. | 当F=0时,f1=f2=10N | B. | 当F=50N时,f1=0,f2=5N | ||
| C. | 当F=100N时,f1=5N,f2=10N | D. | 当F=300N时,f1=10N,f2=20N |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图甲,100匝的线圈(图中只画了2匝)两端A、B与一个阻值R=48Ω的电阻相连,其线圈的电阻r=2Ω,线圈内有指向纸内方向的磁场,线圈中的磁通量在按图乙所示规律变化.
如图甲,100匝的线圈(图中只画了2匝)两端A、B与一个阻值R=48Ω的电阻相连,其线圈的电阻r=2Ω,线圈内有指向纸内方向的磁场,线圈中的磁通量在按图乙所示规律变化.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受沿x正方向大小为F的力的作用从静止开始做匀加速直线运动,经过时间t质点运动到A点,A、O两点距离为d,在A点作用力突然变为沿y轴正方向,大小仍为F,再经时间t质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向.求:
如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受沿x正方向大小为F的力的作用从静止开始做匀加速直线运动,经过时间t质点运动到A点,A、O两点距离为d,在A点作用力突然变为沿y轴正方向,大小仍为F,再经时间t质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com