
| A. | 探测器的线速度v=$\frac{2πR}{T}$ | |
| B. | 探测器的角速度ω=$\frac{2π}{T}$ | |
| C. | 探测器的向心加速度a=G$\frac{m}{(R+h)^{2}}$ | |
| D. | 火星表面重力加速度g=$\frac{4{π}^{2}(R+h)^{3}}{{R}^{2}{T}^{2}}$ |
分析 根据万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}r}{{T}^{2}}$,求解中心天体质量,根据v=$\frac{2πr}{T}$求线速度,根据a=$\frac{4{π}^{2}}{{T}^{2}}$r求向心加速度,根据万有引力等于重力,得到火星表面重力加速度.
解答 解:A、探测器运行的线速度 v=$\frac{2πr}{T}$=$\frac{2π(R+h)}{T}$.故A错误;
B、根据角速度与周期的关系公式可知,探测器的角速度ω=$\frac{2π}{T}$.故B正确;
C、向心加速度a=r($\frac{2π}{T}$)2=$\frac{4{π}^{2}(R+h)}{{T}^{2}}$.故C错误
D、探测器绕火星做匀速圆周运动,由万有引力提供向心力,则得:
G$\frac{Mm}{{r}^{2}}$=m($\frac{2π}{T}$)2r,此时r=R+h,
解得火星质量为:M=$\frac{{4{π^2}{{(R+h)}^3}}}{{G{T^2}}}$,
物体在火星表面自由下落的加速度等于火星表面的重力加速度.
根据万有引力等于重力有:G $\frac{Mm′}{{R}^{2}}$=m′g,
解得:g=$\frac{GM}{{R}^{2}}$=$\frac{4{π}^{2}(R+h)^{3}}{{T}^{2}{R}^{2}}$,故D正确.
故选:BD
点评 解决本题的关键掌握卫星问题中两种基本的解题思路:万有引力提供向心力G$\frac{Mm}{(R+h)^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$(R+h),以及万有引力等于重力G$\frac{Mm′}{{R}^{2}}$=m′g.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:选择题
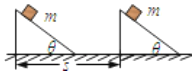 如图所示,质量为m的物体静止在倾角为θ的粗糙斜面上,当斜面沿水平方向向右匀速移动了距离s时,物体m相对斜面静止,则下列说法中不正确的是( )
如图所示,质量为m的物体静止在倾角为θ的粗糙斜面上,当斜面沿水平方向向右匀速移动了距离s时,物体m相对斜面静止,则下列说法中不正确的是( )| A. | 弹力对物体m做正功 | B. | 合力对物体m做功为零 | ||
| C. | 摩擦力对物体m做正功 | D. | 重力对物体m做功为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
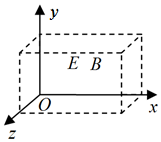 在图中虚线所示的区域存在匀强电场和匀强磁场,取坐标如图.一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转.不计重力影响,电场强度E和磁场强度B的方向可能是( )
在图中虚线所示的区域存在匀强电场和匀强磁场,取坐标如图.一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转.不计重力影响,电场强度E和磁场强度B的方向可能是( )| A. | E和B都沿x轴方向 | B. | E沿y轴正向,B沿z轴正向 | ||
| C. | E沿z轴正向,B沿y轴正向 | D. | E沿z轴正向,B沿y轴负向 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
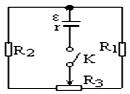 如图所示电路,已知电源电动势E=6.3V,内电阻r=0.5Ω,固定电阻R1=2Ω,R2=3Ω,R3是阻值为5Ω的滑动变阻器.按下电键K,调节滑动变阻器的触点,则通过电源的电流可能是以下哪些值( )
如图所示电路,已知电源电动势E=6.3V,内电阻r=0.5Ω,固定电阻R1=2Ω,R2=3Ω,R3是阻值为5Ω的滑动变阻器.按下电键K,调节滑动变阻器的触点,则通过电源的电流可能是以下哪些值( )| A. | 1.8A | B. | 2.1A | C. | 2.2A | D. | 2.9A |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 电场线的疏密程度表示电场的强弱 | |
| B. | 同一电场中任意两条电场线不相交 | |
| C. | 电场线上某点的切线方向就是放在该点的点电荷所受电场力的方向 | |
| D. | 带电粒子在只受电场力时,运动轨迹一定与电场线重合 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 由质点简谐运动的图象可知质点振动的振幅和频率 | |
| B. | 两列水波在水面上相遇叠加时,必然能形成干涉图样 | |
| C. | 单摆的振动周期与摆球质量和振幅无关 | |
| D. | 机械波从一种介质传播到另一介质时,频率变化,速度变化 | |
| E. | 当观察者与声源靠近时,听到的声音频率大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
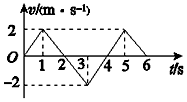
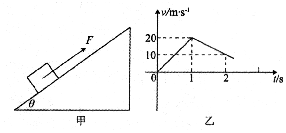
| A. | 在第2秒末加速度方向发生了改变 | B. | 在第2秒末速度方向发生了改变 | ||
| C. | 第3秒末和第5秒末的位置相同 | D. | 在前2秒内发生的位移为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com