
分析 (1)根据火星与地球的半径和质量关系求得引力的倍数关系;
(2)星球的第一宇宙速度为绕星球表面圆周运动的线速度,根据火星与地球半径和质量关系求得宇宙速度的倍数关系.
解答 解:由题意知$\frac{{R}_{火}}{{R}_{地}}=\frac{1}{2}$,$\frac{{M}_{火}}{{M}_{地}}=\frac{1}{10}$
(1)在火星表面探测器受到的引力${F}_{火}=\frac{G{M}_{火}}{{R}_{火}^{2}}$,地球表面探测器受到的引力$;{F}_{地}=\frac{G{M}_{地}m}{{R}_{地}^{2}}$${F}_{地}=\frac{G{M}_{地}m}{{R}_{地}^{2}}$
所以$\frac{{F}_{火}}{{F}_{地}}=\frac{{M}_{火}}{{M}_{地}}•(\frac{{R}_{地}}{{R}_{火}})^{2}$=$\frac{1}{10}×(\frac{2}{1})^{2}$=0.4
即探测器在火星受到引力是地球受到引力的0.4倍;
(2)据万有引力提供圆周运动向心力有$G\frac{mM}{{R}^{2}}=m\frac{{v}^{2}}{R}$可得地球表面的第一宇宙速度${v}_{地}=\sqrt{\frac{G{M}_{地}}{{R}_{地}}}$,同理可得火星表面的第一宇宙速度${v}_{火}=\sqrt{\frac{G{M}_{火}}{{R}_{火}}}$
所以可得:$\frac{{v}_{火}}{{v}_{地}}=\frac{\sqrt{\frac{G{M}_{火}}{{R}_{火}}}}{\sqrt{\frac{G{M}_{地}}{{R}_{地}}}}=\sqrt{\frac{{M}_{火}}{{M}_{地}}}•\sqrt{\frac{{R}_{地}}{{R}_{火}}}$=$\sqrt{\frac{1}{10}}×\sqrt{\frac{2}{1}}$=$\sqrt{\frac{1}{5}}$
即火星第一宇宙速度是地球第一宇宙速度的$\sqrt{\frac{1}{5}}倍$
答:(1)“落”:探测器落到火星表面时,受到的引力为在地球表面时的0.4倍;
(2)“绕”:物体紧贴星球表面绕行时的速度为第一宇宙速度.火星的第一宇宙速度为地球第一宇宙速度的$\sqrt{\frac{1}{5}}倍$.
点评 掌握万有引力定律的表达式,知道第一宇宙速度是围绕星球表面圆周运动的速度,能根据万有引力提供向心力求得第一宇宙速度的表达式是正确解题的关键.


科目:高中物理 来源: 题型:选择题
| A. | 月球表面的重力加速度 | B. | 月球的质量 | ||
| C. | 月球的第一宇宙速度 | D. | 月球对宇航员的引力 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 小球落地点与抛出点的水平距离为9.8m | |
| B. | 小球落地点与抛出点的水平距离为4.9m | |
| C. | 小球落地时的速度大小为4.9m/s | |
| D. | 小球落地时的速度大小为9.8m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
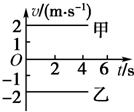 如图为甲、乙两质点的v-t图象.对于甲、乙两质点的运动,下列说法正确的是( )
如图为甲、乙两质点的v-t图象.对于甲、乙两质点的运动,下列说法正确的是( )| A. | 在相同的时间内,质点甲、乙的位移相同 | |
| B. | 质点甲和乙的速度并不相同 | |
| C. | 不管质点甲、乙是否从同一地点开始运动,它们之间的距离一定越来越大 | |
| D. | 质点甲向所选定的正方向运动,质点乙与甲的运动方向相反 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
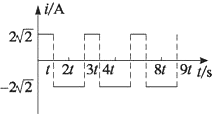
| A. | 2$\sqrt{2}$A | B. | 4 A | C. | 3.5$\sqrt{2}$A | D. | 6 A |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
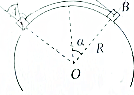 如图,质量为$\frac{\sqrt{3}}{3}$kg的A物体与质量为1kg的B物体(大小忽略),用质量可略细线连接后,放在半径为R的光滑圆柱面上处于平衡状态,已知AB弧长$\frac{πR}{2}$,则OB与竖直方向的夹角α等于( )
如图,质量为$\frac{\sqrt{3}}{3}$kg的A物体与质量为1kg的B物体(大小忽略),用质量可略细线连接后,放在半径为R的光滑圆柱面上处于平衡状态,已知AB弧长$\frac{πR}{2}$,则OB与竖直方向的夹角α等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 以上答案都不对 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
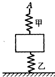 如图所示,物块质量为m,与甲、乙两弹簧相连接,乙弹簧下端与地面连接,甲、乙两弹簧质量不计,其劲度系数分别为k1、k2,起初甲弹簧处于自由长度,现用手将甲弹簧的A端缓慢上提,使乙弹簧产生的弹力大小变为原来的$\frac{2}{3}$,则A端上移距离可能是( )
如图所示,物块质量为m,与甲、乙两弹簧相连接,乙弹簧下端与地面连接,甲、乙两弹簧质量不计,其劲度系数分别为k1、k2,起初甲弹簧处于自由长度,现用手将甲弹簧的A端缓慢上提,使乙弹簧产生的弹力大小变为原来的$\frac{2}{3}$,则A端上移距离可能是( )| A. | $\frac{{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | B. | $\frac{2{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | ||
| C. | $\frac{4{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | D. | $\frac{5{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
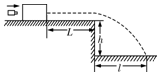 如图所示,质量为M=0.2kg的木块放在水平台面上,水平台面比水平地面高出h=0.2m,木块距水平台面的右端L=1.7m.质量为m=0.1M的子弹以v0=180m/s的速度水平射向木块,当子弹以v=90m/s的速度水平射出时,木块的速度为v1=9m/s(此过程作用时间极短,可认为木块的位移为零).若木块落到水平地面时的落地点到水平台面右端的水平距离为l=1.6m,求:(g取10m/s2)
如图所示,质量为M=0.2kg的木块放在水平台面上,水平台面比水平地面高出h=0.2m,木块距水平台面的右端L=1.7m.质量为m=0.1M的子弹以v0=180m/s的速度水平射向木块,当子弹以v=90m/s的速度水平射出时,木块的速度为v1=9m/s(此过程作用时间极短,可认为木块的位移为零).若木块落到水平地面时的落地点到水平台面右端的水平距离为l=1.6m,求:(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,两根固定的光滑硬杆OA与OB,夹角为θ,各套轻环C,D且C,D用细绳相连,现用一恒力F沿OB方向拉环C,当两环平衡时,绳子的拉力是$\frac{F}{sinθ}$.
如图所示,两根固定的光滑硬杆OA与OB,夹角为θ,各套轻环C,D且C,D用细绳相连,现用一恒力F沿OB方向拉环C,当两环平衡时,绳子的拉力是$\frac{F}{sinθ}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com