
 如图所示,一带正电粒子质量为m,带电量为q,从隔板ab上一个小孔P处于隔板成45°角垂直于磁感线射入磁感应强度为B的单边界匀强磁场,粒子初速度大小为v,不计粒子的重力,则:
如图所示,一带正电粒子质量为m,带电量为q,从隔板ab上一个小孔P处于隔板成45°角垂直于磁感线射入磁感应强度为B的单边界匀强磁场,粒子初速度大小为v,不计粒子的重力,则:分析 粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出粒子的轨道半径,应用粒子周期公式与几何知识分析答题.
解答 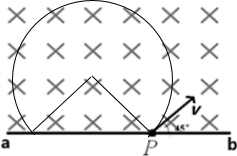 解:(1)粒子在磁场中做匀速圆周运动,由左手定则,轨迹如图所示:
解:(1)粒子在磁场中做匀速圆周运动,由左手定则,轨迹如图所示:
由几何知识可知,粒子转过的圆心角:θ=270°,
打到隔板上时距出发点P的距离:d=2rsin45°
粒子在磁场中运动由洛伦兹力提供圆周运动向心力有:
$qvB=m\frac{{v}^{2}}{r}$
可得圆周运动轨道半径为:r=$\frac{mv}{qB}$
所以粒子再次到达隔板距离P点距离为:d=$\sqrt{2}\frac{mv}{qB}$
(2)粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,
粒子在磁场中的运动时间:t=$\frac{θ}{360°}T=\frac{270°}{360°}×\frac{2πm}{qB}$=$\frac{3πm}{2qB}$
答:(1)粒子再次到达隔板距离P点为$\sqrt{2}\frac{mv}{qB}$;
(2)粒子经过$\frac{3πm}{2qB}$时间再次到达隔板.
点评 本题考查了粒子在磁场中的运动,粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,分析清楚粒子运动过程,应用牛顿第二定律与周期公式即可正确解题.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某实验探究小组为了测定滑动变阻器上金属丝的电阻率,除待测滑动变阻器Rx(总阻值约25Ω)外,在实验室还找到了下列器材.
某实验探究小组为了测定滑动变阻器上金属丝的电阻率,除待测滑动变阻器Rx(总阻值约25Ω)外,在实验室还找到了下列器材.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为2.5cm,如果取g=10m/s2,那么:
如图所示为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为2.5cm,如果取g=10m/s2,那么:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | m1>m2 | B. | F1<F2 | C. | $\frac{{F}_{1}}{{m}_{1}}$<$\frac{{F}_{2}}{{m}_{2}}$ | D. | $\frac{{F}_{1}}{{m}_{1}}$>$\frac{{F}_{2}}{{m}_{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l=0.5m,左端接有阻值R=0.3Ω的电阻.一质量m=0.1kg,电阻r=0.1Ω的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=0.4T.棒在水平向右的外力作用下,由静止开始以a=2m/s2的加速度做匀加速运动,当棒的位移为x时撤去外力,此过程通过电阻R的电荷量q=4.5C.,棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比Q1:Q2=2:1.导轨足够长且电阻不计,棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触.求:
如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l=0.5m,左端接有阻值R=0.3Ω的电阻.一质量m=0.1kg,电阻r=0.1Ω的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=0.4T.棒在水平向右的外力作用下,由静止开始以a=2m/s2的加速度做匀加速运动,当棒的位移为x时撤去外力,此过程通过电阻R的电荷量q=4.5C.,棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比Q1:Q2=2:1.导轨足够长且电阻不计,棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示是一种延时开关,当S1闭合时,电磁铁F将衔铁D吸下,C线路接通;当S1断开时,由于电磁感应作用,D将延迟一段时间才被释放,则( )
如图所示是一种延时开关,当S1闭合时,电磁铁F将衔铁D吸下,C线路接通;当S1断开时,由于电磁感应作用,D将延迟一段时间才被释放,则( )| A. | 由于A线圈的电磁感应作用,才产生延时释放D的作用 | |
| B. | 由于B线圈的电磁感应作用,才产生延时释放D的作用 | |
| C. | 如果断开B线圈的电键S2,仍有延时作用 | |
| D. | 如果断开B线圈的电键S2,延时将变长 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com