
 ��ͼ��ʾ�����浼��Ļ����ϰ�װ�˿���Ϊd���ڹ�壬�������˶��Ļ����Ⱥ�ͨ����������ţ����ֺ���Ƽ�¼���ڹ��ͨ����һ������ŵ�ʱ��Ϊt1��ͨ���ڶ�������ŵ�ʱ��Ϊt2���ڹ��ӿ�ʼ��ס��һ������ŵ���ʼ��ס�ڶ�������ŵ�ʱ��Ϊ��t�����в����������ӽ���ʵֵ���ǣ�������
��ͼ��ʾ�����浼��Ļ����ϰ�װ�˿���Ϊd���ڹ�壬�������˶��Ļ����Ⱥ�ͨ����������ţ����ֺ���Ƽ�¼���ڹ��ͨ����һ������ŵ�ʱ��Ϊt1��ͨ���ڶ�������ŵ�ʱ��Ϊt2���ڹ��ӿ�ʼ��ס��һ������ŵ���ʼ��ס�ڶ�������ŵ�ʱ��Ϊ��t�����в����������ӽ���ʵֵ���ǣ�������| A�� | �����˶��ļ��ٶ�Ϊ$\frac{{d��{t_1}-{t_2}��}}{{{t_1}{t_2}����t��}}$ | |
| B�� | �����˶��ļ��ٶ�Ϊ$\frac{{2d��{t_1}-{t_2}��}}{{{t_1}{t_2}[{2����t��+{t_2}-{t_1}}]}}$ | |
| C�� | �ڹ���е�ͨ����һ������ŵ��ٶ�Ϊ$\frac{d}{t_1}$ | |
| D�� | �ڹ��ǰ��ͨ����һ������ŵ��ٶ�Ϊ$\frac{d}{t_1}$ |
���� ���ݼ���ʱ���ڵ�ƽ���ٶȵ����м�ʱ�̵�˲ʱ�ٶ���������м�ʱ�̵�˲ʱ�ٶȣ�����ٶ�ʱ�乫ʽ�������ļ��ٶȣ�
��� �⣺A������ij��ʱ���ڵ�ƽ���ٶȵ����м�ʱ�̵�˲ʱ�ٶ�֪������ͨ������������м�ʱ�̵�˲ʱ�ٶȷֱ�Ϊ��${v}_{1}=\frac{d}{{t}_{1}}$��${v}_{2}=\frac{d}{{t}_{2}}$��
�����м�ʱ�̵�ʱ���Ϊ��$t=��t-\frac{{t}_{1}}{2}+\frac{{t}_{2}}{2}$��
�����ٶ�ʱ�乫ʽ�ã������˶��ļ��ٶ�Ϊ��a=$\frac{{v}_{2}-{v}_{1}}{t}=\frac{\frac{d}{{t}_{2}}-\frac{d}{{t}_{1}}}{��t-\frac{{t}_{1}}{2}+\frac{{t}_{2}}{2}}$=$\frac{{2d��{t_1}-{t_2}��}}{{{t_1}{t_2}[{2����t��+{t_2}-{t_1}}]}}$����B��ȷ��A����
C���ڹ��ͨ����һ��������м�ʱ�̵�˲ʱ�ٶ�Ϊ$\frac{d}{{t}_{1}}$���м�ʱ�̵�˲ʱ�ٶ�С���м�λ�õ�˲ʱ�ٶȣ����ڹ���е�ͨ����һ������ŵ��ٶȴ���$\frac{d}{{t}_{1}}$���ڹ��ǰ��ͨ����һ������ŵ��ٶ�С��$\frac{d}{{t}_{1}}$����CD����
��ѡ��B��
���� �������Ĺؼ������ȱ���ֱ���˶����˶�ѧ��ʽ�����ۣ�����������ã�ע�Ȿ�ⲻ����ij��ʱ���ڵ�ƽ���ٶȵ���˲ʱ�ٶȷ�����⣬��Ϊ�ڹ��ij��Ȳ��Ạ̊́ܶ��Լ�ע�������������ӽ���ʵֵ�ģ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
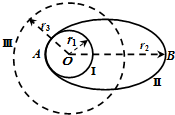 ��������ΪM���뾶ΪR����ת����ΪT0��ȡ����Զ������������Ϊ�㣮����Ϊm���������Ƶ�����������ʱ�����͵�����ɵ�ϵͳ��е���غ㣬����֮���������ܵı���ʽ��Ep=-$\frac{GMm}{r}$������r����������ļ�ľ��룮����������Ϊm�����Ǵӽ���Բ������䵽��Բ�������ȥ�������Ľ��ص�A��Զ�ص�B����ķֱ�Ϊr1=R��r2=3R���������ڹ�����ϵĻ�е�ܺ���r3=2R��Բ�ܹ�����ϵĻ�е����ͬ��������
��������ΪM���뾶ΪR����ת����ΪT0��ȡ����Զ������������Ϊ�㣮����Ϊm���������Ƶ�����������ʱ�����͵�����ɵ�ϵͳ��е���غ㣬����֮���������ܵı���ʽ��Ep=-$\frac{GMm}{r}$������r����������ļ�ľ��룮����������Ϊm�����Ǵӽ���Բ������䵽��Բ�������ȥ�������Ľ��ص�A��Զ�ص�B����ķֱ�Ϊr1=R��r2=3R���������ڹ�����ϵĻ�е�ܺ���r3=2R��Բ�ܹ�����ϵĻ�е����ͬ��������| A�� | �����ڽ���Բ����������е������������ת������ͬ | |
| B�� | �ӹ�����䵽�������Ҫ�ڽ��ص�A��һ���Ը����ṩ����$\frac{GMm}{4R}$ | |
| C�� | ��������Բ����ϵ�����ΪT0$\sqrt{��\frac{{r}_{2}+R}{R}��^{3}}$ | |
| D�� | ��������Բ���������������ʱ������B��Ļ�е�ܴ�����A��Ļ�е�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
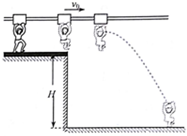 ij�������ֽ�Ŀ��������ǰ�塱�ij�����ʩ��ͼ���㹻����ˮƽ������װ�п��ظ����ɻ��������������������뻬�˵Ķ�Ħ������Ϊ��=0.2��ѡ������ظ�H=5m��ƽ̨�ϣ�ץס����������һ����������ܣ��ɻ�ó��ٶȲ�����ƽ̨��Ϊ�����ڵ�����ʵ�λ�ã�ѡ�ֱ��������жϣ��ں��ʵ�ʱ��λ�÷ſ���������gȡ10m/s2��
ij�������ֽ�Ŀ��������ǰ�塱�ij�����ʩ��ͼ���㹻����ˮƽ������װ�п��ظ����ɻ��������������������뻬�˵Ķ�Ħ������Ϊ��=0.2��ѡ������ظ�H=5m��ƽ̨�ϣ�ץס����������һ����������ܣ��ɻ�ó��ٶȲ�����ƽ̨��Ϊ�����ڵ�����ʵ�λ�ã�ѡ�ֱ��������жϣ��ں��ʵ�ʱ��λ�÷ſ���������gȡ10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
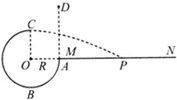 ��ͼ��ʾ���뾶ΪR�Ĺ⻬Բ�����ABC�̶�����ֱƽ���ڣ�O��Բ�ģ�OC��ֱ��OAˮƽ��B����͵㣬A�����һ�㹻����ƽ̨MN��D��λ��A�����Ϸ���DA����Ϊ����ֵ������D�����ٶ��ͷ�һ����С���Ժ��Ե�С����A�����Բ���������C��ɳ�����ƽ���˶�������ƽ̨MN�ϣ�P����С������MN֮ǰ�켣�Ͻ���MN��һ�㣬���ƿ�������������˵����ȷ���ǣ�������
��ͼ��ʾ���뾶ΪR�Ĺ⻬Բ�����ABC�̶�����ֱƽ���ڣ�O��Բ�ģ�OC��ֱ��OAˮƽ��B����͵㣬A�����һ�㹻����ƽ̨MN��D��λ��A�����Ϸ���DA����Ϊ����ֵ������D�����ٶ��ͷ�һ����С���Ժ��Ե�С����A�����Բ���������C��ɳ�����ƽ���˶�������ƽ̨MN�ϣ�P����С������MN֮ǰ�켣�Ͻ���MN��һ�㣬���ƿ�������������˵����ȷ���ǣ�������| A�� | ֻҪD��ĸ߶Ⱥ��ʣ�С���������ƽ̨MN������һ�� | |
| B�� | С���A�˶���B�Ĺ����У������Ĺ���һֱ���� | |
| C�� | С����D��A��B��C��P�Ĺ����У�����D��Ļ�е�ܴ���P��Ļ�е�� | |
| D�� | ���DA����Ϊh����С��B��ʱ�Թ����ѹ��Ϊ3mg+$\frac{2mgh}{R}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
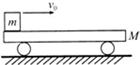 ��ͼ��ʾ������ΪM=3kg��ƽ��С����ֹ�ڹ⻬��ˮƽ���ϣ�С��ƽ���������ĸ߶�h=1.8m����һ����m=1kg��С��飨����Ϊ�ʵ㣩��v0=5m/s��С����˻���С������С�����˶�2s��С���Ҷ˷ɳ����������ˮƽ�����ϣ���û��黬��С������ع����е�ˮƽλ�ƴ�СΪs=8.2m���������ٶ�Ϊg=10m/s2����
��ͼ��ʾ������ΪM=3kg��ƽ��С����ֹ�ڹ⻬��ˮƽ���ϣ�С��ƽ���������ĸ߶�h=1.8m����һ����m=1kg��С��飨����Ϊ�ʵ㣩��v0=5m/s��С����˻���С������С�����˶�2s��С���Ҷ˷ɳ����������ˮƽ�����ϣ���û��黬��С������ع����е�ˮƽλ�ƴ�СΪs=8.2m���������ٶ�Ϊg=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�����ΪL�ĵ���A��B�������ֱ�Ϊ+4Q��-Q�����������������C��ʹ�������ɶ�����ƽ��״̬����C�ĵ����ͷ��õ�λ���ǣ�������
��ͼ��ʾ�����ΪL�ĵ���A��B�������ֱ�Ϊ+4Q��-Q�����������������C��ʹ�������ɶ�����ƽ��״̬����C�ĵ����ͷ��õ�λ���ǣ�������| A�� | -Q����A����AΪL�� | B�� | -2Q����A����AΪ$\frac{L}{2}$�� | ||
| C�� | +2Q����B�Ҳ��B Ϊ$\frac{3L}{2}$�� | D�� | +4Q����B�Ҳ��BΪL�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 һ�⾵�Ľ���Ϊֱ��������ABC�����С�A=30�㣬�ڴ˽������ڵ�ƽ���ڣ�һ��������i=45�������Ǵ�AC�ߵ��е�M�����⾵������һ�������ȫ�����ֱ��BC�ߴ�E���������
һ�⾵�Ľ���Ϊֱ��������ABC�����С�A=30�㣬�ڴ˽������ڵ�ƽ���ڣ�һ��������i=45�������Ǵ�AC�ߵ��е�M�����⾵������һ�������ȫ�����ֱ��BC�ߴ�E����������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
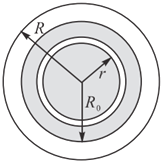 �趨������һ���������ȷֲ������壬��֪�����ֲ����ȵ���Ƕ����ڲ����������Ϊ�㣮��ͼ��ʾ���п�ѧ�������ڵ����ڲ���һ���뾶Ϊr�Ļ��ι�����ڻ��ι���ڷ���һ�����조���ǡ�A�����조���ǡ�������������������������Բ���˶������ڵ����Ͽշ���һ�Ź���뾶ΪR�������������B����֪����뾶ΪRo�������й��ڡ����ǡ�A������B�˶������ļ��ٶȴ�С�����ٶȴ�С�����ٶȡ�����֮����ȷ���ǣ�������
�趨������һ���������ȷֲ������壬��֪�����ֲ����ȵ���Ƕ����ڲ����������Ϊ�㣮��ͼ��ʾ���п�ѧ�������ڵ����ڲ���һ���뾶Ϊr�Ļ��ι�����ڻ��ι���ڷ���һ�����조���ǡ�A�����조���ǡ�������������������������Բ���˶������ڵ����Ͽշ���һ�Ź���뾶ΪR�������������B����֪����뾶ΪRo�������й��ڡ����ǡ�A������B�˶������ļ��ٶȴ�С�����ٶȴ�С�����ٶȡ�����֮����ȷ���ǣ�������| A�� | $\frac{{a}_{A}}{{a}_{B}}$=��$\frac{R}{r}$��2 | B�� | $\frac{{v}_{A}}{{v}_{B}}$=$\frac{r}{{R}_{0}}$$\sqrt{\frac{R}{{R}_{0}}}$ | C�� | $\frac{{��}_{A}}{{��}_{B}}$=$\frac{R}{{R}_{0}}$$\sqrt{\frac{R}{{R}_{0}}}$ | D�� | $\frac{{T}_{A}}{{T}_{B}}$=$\frac{R}{r}$$\sqrt{\frac{R}{r}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | $\frac{3}{4}$�� | B�� | $\frac{4}{3}$�� | C�� | $\frac{3}{2}$�� | D�� | 2�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com