
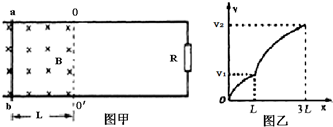
分析 (1)根据法拉第电磁感应定律列式求解平均感应电动势,根据闭合电路欧姆定律求解平均电流,根据电流的定义求解电量q;
(2)对杆运动L的过程运用功能关系列式,对接下来的2L位移过程再次根据动能定理列式,根据焦耳定律得到电阻R上产生的焦耳热与电路中总的焦耳热的关系,最后联立求解;
(3)磁场旋转时,可等效为矩形闭合电路在匀强磁场中反方向匀速转动,根据Em=BSω求解最大值,根据$E=\frac{{E}_{m}}{\sqrt{2}}$求解有效值,最后根据焦耳定律列式求解.
解答 解:(1)根据法拉第电磁感应定律,有:
$E=\frac{△Φ}{△t}=\frac{B}{t}{L^2}$
根据闭合电路欧姆定律,有:
$I=\frac{E}{R+r}$
电量:
q=It
联立解得:
$q=\frac{{B{L^2}}}{R+r}$
(2)ab杆由起始位置发生位移L的过程,根据功能关系,有:
$FL=\frac{1}{2}mv_1^2+{Q_总}$
ab杆从L到3L的过程中,由动能定理可得:
$2FL=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2$
联立解得:
${Q_总}=\frac{m(v_2^2-3v_1^2)}{4}$
根据焦耳定律,有:
${Q_1}=\frac{R}{R+r}$Q总
联立解得:
${Q_1}=\frac{Rm(v_2^2-3v_1^2)}{4(R+r)}$
(3)磁场旋转时,可等效为矩形闭合电路在匀强磁场中反方向匀速转动,所以闭合电路中产生正弦式电流,感应电动势的峰值:
${E_m}=BSω=B{L^2}ω$
有效值:
$E=\frac{E_m}{{\sqrt{2}}}$
根据焦耳定律,有:
${Q_2}=\frac{E^2}{R+r}•\frac{T}{4}$
而$T=\frac{2π}{ω}$,则:
$ω=\frac{{4(R+r){Q_2}}}{{π{B^2}{L^4}}}$
答:(1)此过程中电阻R上产生的电量q为$\frac{B{L}^{2}}{R+r}$.
(2)此过程中电阻R上产生的焦耳热为$\frac{Rm({v}_{2}^{2}-3{v}_{1}^{2})}{4(R+r)}$.
(3)磁场转动的角速度ω大小是$\frac{4(R+r){Q}_{2}}{π{B}^{2}{L}^{4}}$.
点评 本题关键是区分交流四值,知道求解电量用平均值、求解热量用有效值,同时要结合法拉第电磁感应定律和闭合电路欧姆定律列式求解,不难.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中物理 来源: 题型:解答题
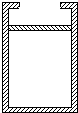 如图所示,开口处有卡口、内截面积为S的导热性能良好的圆柱形气缸开口向上竖直放置在水平面上,缸内总体积为V0,大气压强为p0,一厚度不计、质量为m的活塞(m=0.2p0S/g)封住一定量的理想气体,温度为T0时缸内气体体积为0.8V0,先在活塞上缓慢放上质量为2m的砂子,然后逐渐升高缸内气体温度,求:
如图所示,开口处有卡口、内截面积为S的导热性能良好的圆柱形气缸开口向上竖直放置在水平面上,缸内总体积为V0,大气压强为p0,一厚度不计、质量为m的活塞(m=0.2p0S/g)封住一定量的理想气体,温度为T0时缸内气体体积为0.8V0,先在活塞上缓慢放上质量为2m的砂子,然后逐渐升高缸内气体温度,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
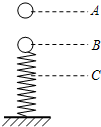 一小球自A点由静止自由下落 到B点时与弹簧接触,到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )
一小球自A点由静止自由下落 到B点时与弹簧接触,到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )| A. | 小球在B点时动能最大 | |
| B. | 小球的重力势能不断增大 | |
| C. | 小球和弹簧组成的系统机械能守恒 | |
| D. | 到C点时小球重力势能的减少量等于弹簧弹性势能的增加量 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 地球质量M=$\frac{a{R}^{2}}{G}$ | B. | 地球密度$ρ=\frac{{3{a_1}r_1^2}}{{4πG{R^3}}}$ | ||
| C. | 地球的第一宇宙速度为$\sqrt{aR}$ | D. | 向心加速度之比$\frac{{a}_{1}}{a}$=$\frac{{R}^{2}}{{{r}_{1}}^{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{v_0}{t}$ | B. | $\sqrt{\frac{{{v_0}R}}{t}}$ | C. | $\sqrt{\frac{{2{v_0}R}}{t}}$ | D. | $\sqrt{\frac{v_0}{Rt}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 摩擦力对物体做功10J | B. | 摩擦力对物体做功-10J | ||
| C. | 摩擦力不做功 | D. | 物体克服摩擦力做功10J |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
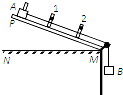 如图所示,NM是水平桌面,PM是一端带有滑轮的长木板,1、2是固定在木板上的两个光电门.质量为M的滑块A上固定一遮光条,在质量为m的重物B牵引下从木板的顶端由静止滑下,光电门1、2记录遮光时间分别为△t1和△t2.(重力加速度为g)
如图所示,NM是水平桌面,PM是一端带有滑轮的长木板,1、2是固定在木板上的两个光电门.质量为M的滑块A上固定一遮光条,在质量为m的重物B牵引下从木板的顶端由静止滑下,光电门1、2记录遮光时间分别为△t1和△t2.(重力加速度为g)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com