
分析 (1)根据实验中误差产生的原因,明确实验中应注意的事项.
(2)用尽可能小的圆把各落点圈起来,该圆的圆心可以作为小球落点的平均位置.
(3)根据动量守恒定律求出需要验证的表达式.
(4)小球落在斜面上,根据水平位移关系和竖直位移的关系,求出初速度与距离的表达式,从而得出动量守恒的表达式.
解答 解:(1)A、轨道是否光滑对实验的结果没有影响,不需要控制轨道光滑,故A错误;
B、要保证碰撞后两个球做平抛运动,故斜槽轨道末端的切线必须水平,故B正确;
C、为保证碰撞的初速度相同,入射球每次必须从轨道的同一位置由静止滚下,故C正确;
D、碰撞后为防止入射球反弹,入射球的质量应大于被碰球的质量,即小球A质量应大于小球B的质量,故D正确;
故选:BCD;
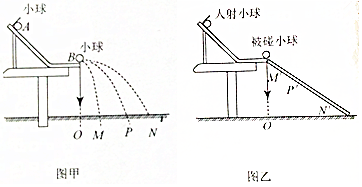
(2)为减小实验误差,应用尽可能小的圆将小球所有落点圈在里面,该圆的圆心位置即为落点平均位置;
(3)小球离开斜槽后做平抛运动,由于抛出点的高度相等,它们做平抛运动的时间t相等,
以向右为正方向,如果碰撞过程动量守恒,由动量守恒定律得:m1v1=m1v1′+m2v2′,
两边同时乘以时间t得:m1v1t=m1v1′t+m2v2′t,即:m1OP=m1OM+m2′ON,
需要验证的表达式为:m1OP=m1OM+m2ON;
(4)碰撞前,m1落在图中的P′点,设其水平初速度为v1.小球m1和m2发生碰撞后,m1的落点在图中M′点,设其水平初速度为v1′,m2的落点是图中的N′点,设其水平初速度为v2. 设斜面BC与水平面的倾角为α,
由平抛运动规律得:l1sinα=$\frac{1}{2}$gt2,l1cosα=v1t,解得:v1=$\sqrt{\frac{g{l}_{2}co{s}^{2}α}{2sinα}}$,
同理可知:v1′=$\sqrt{\frac{g{l}_{1}co{s}^{2}α}{2sinα}}$,v2′=$\sqrt{\frac{g{l}_{3}co{s}^{2}α}{2sinα}}$,
如果碰撞过程动量守恒,则:m1v1=m1v1′+m2v2′,
即m1$\sqrt{\frac{g{l}_{2}co{s}^{2}α}{2sinα}}$=m1$\sqrt{\frac{g{l}_{1}co{s}^{2}α}{2sinα}}$+m2$\sqrt{\frac{g{l}_{3}co{s}^{2}α}{2sinα}}$,
整理得:m1$\sqrt{{l}_{2}}$=m1$\sqrt{{l}_{1}}$+m2$\sqrt{{l}_{3}}$,实验需要验证:
故答案为.(1)BCD;(2)用尽可能小的圆将小球所有落点圈在里面,该圆的圆心位置即为落点平均位置;
(3)m1OP=m1OM+m2ON;(4)m1$\sqrt{{l}_{2}}$=m1$\sqrt{{l}_{1}}$+m2$\sqrt{{l}_{3}}$.
点评 解决本题的关键掌握实验的原理,以及实验的步骤,在验证动量守恒定律实验中,无需测出速度的大小,可以用位移代表速度.同时,在运用平抛运动的知识得出碰撞前后两球的速度,因为下落的时间相等,则水平位移代表平抛运动的速度.若碰撞前后总动能相等,则机械能守恒.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中物理 来源: 题型:多选题
| A. | 甲球的速度为零而乙球的速度不为零 | |
| B. | 乙球的速度为零而甲球的速度不为零 | |
| C. | 两球的速度均不为零 | |
| D. | 两球的速度均与原方向相反,两球的动能仍相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
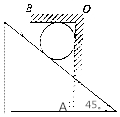 如图所示,倾角为45°直角三角形劈水平放置,质量为m的光滑圆球放在劈的斜面上,被固定在劈上的直角挡板AOB挡住,静止时,圆球顶部与水平挡板OB接触但无弹力.某时刻三角形劈在外力作用下先向左加速一段时间,然后改做加速度大小为a的减速运动,重力加速度为g,面说法正确的是( )
如图所示,倾角为45°直角三角形劈水平放置,质量为m的光滑圆球放在劈的斜面上,被固定在劈上的直角挡板AOB挡住,静止时,圆球顶部与水平挡板OB接触但无弹力.某时刻三角形劈在外力作用下先向左加速一段时间,然后改做加速度大小为a的减速运动,重力加速度为g,面说法正确的是( )| A. | 当球静止时,球对AO挡板的作用力FAO=$\sqrt{2}$mg | |
| B. | 减速阶段,当a=g时球对AO挡板的作用力FAO=mg | |
| C. | 减速阶段,当a>g时球对BO挡板的作用力FBO=m(a-g) | |
| D. | 减速阶段,当a<g时球对BO挡板的作用力FBO=m(g-a) |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
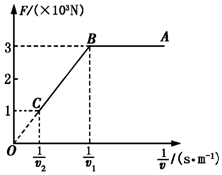 一辆汽车质量为2×103kg,额定功率为3×104W.在水平路面由静止开始作直线运动,运动中汽车所受阻力恒定,发动机的最大牵引力为3×103N,汽车以额定功率行驶100s时速度达到最大,其行驶过程中牵引力F与车速的倒数$\frac{1}{v}$的关系如图所示,求:
一辆汽车质量为2×103kg,额定功率为3×104W.在水平路面由静止开始作直线运动,运动中汽车所受阻力恒定,发动机的最大牵引力为3×103N,汽车以额定功率行驶100s时速度达到最大,其行驶过程中牵引力F与车速的倒数$\frac{1}{v}$的关系如图所示,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
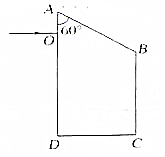 如图所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD射入.已知棱镜的折射率n=$\sqrt{2}$,AB=BC=6cm,OA=1.5cm,∠OAB=60°,求:
如图所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD射入.已知棱镜的折射率n=$\sqrt{2}$,AB=BC=6cm,OA=1.5cm,∠OAB=60°,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 牛顿建立了“日心说” | |
| B. | 爱因斯坦发现万有引力定律 | |
| C. | 卡文迪许最早测出引力常量 | |
| D. | 伽利略发现了太阳系行星运动三大定律 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
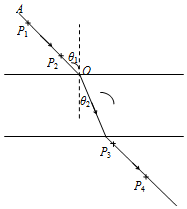 某同学利用“插针法”测定玻璃的折射率,所用的玻璃砖两面平行.正确操作后,作出的光路图及测出的相关角度如图所示.
某同学利用“插针法”测定玻璃的折射率,所用的玻璃砖两面平行.正确操作后,作出的光路图及测出的相关角度如图所示.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
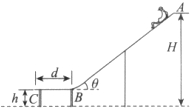 水上滑梯可简化成如图所示的模型,倾角为θ=37°斜滑道AB和水平滑道BC平滑连接.起点A距水面的高度H=8.0m,BC长d=2.0m,端点C距水面的高度h=2.0m,一质量m=60kg的运动员从滑道起点A点无初速地自由滑下,不计空气阻力(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点).已知运动员与AB、BC间有摩擦力,且动摩擦因数均为μ=0.15,求:
水上滑梯可简化成如图所示的模型,倾角为θ=37°斜滑道AB和水平滑道BC平滑连接.起点A距水面的高度H=8.0m,BC长d=2.0m,端点C距水面的高度h=2.0m,一质量m=60kg的运动员从滑道起点A点无初速地自由滑下,不计空气阻力(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点).已知运动员与AB、BC间有摩擦力,且动摩擦因数均为μ=0.15,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com