
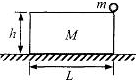
 ��ͼ��ʾ��һ�ϱ���⻬�ľ��λ�������ˮƽ�����ϣ�������M=2kg����L=2m����h=0.8m�����������䶯Ħ��������=0.2���ڻ�����Ҷ˷���һ����m=1kg��С����������������ˣ�ʹ���ڼ���ʱ���ڻ��v0=4m/s��ˮƽ�����ٶȣ�����һ��ʱ���С����أ���gȡ10m/s2������
��ͼ��ʾ��һ�ϱ���⻬�ľ��λ�������ˮƽ�����ϣ�������M=2kg����L=2m����h=0.8m�����������䶯Ħ��������=0.2���ڻ�����Ҷ˷���һ����m=1kg��С����������������ˣ�ʹ���ڼ���ʱ���ڻ��v0=4m/s��ˮƽ�����ٶȣ�����һ��ʱ���С����أ���gȡ10m/s2���������� ��1������ţ�ٵڶ����������ٶȴ�С��
��2������λ���ٶȹ�ϵ���С���뿪����ʱ������ٶȴ�С������С�����������ʱ�䣬�ٸ���λ��ʱ���ϵ���λ�Ƽ��ɣ�
��� �⣺��1�����ڻ����ϱ���⻬����С����ˮƽ�������������ã�����С�����뻬��֮ǰ��С��ʼ�վ�ֹ��
���ڻ��飬����ٶȴ�СΪ��a1=$\frac{�̣�M+m��g}{M}$=$\frac{0.2����2+1��}{2}$��10m/s2=3m/s2��
��2��С�����뻬��ʱ��������ٶ�Ϊv1�����У�${v}_{0}^{2}-{v}_{1}^{2}=2aL$��
�������ݽ�ã�v1=2m/s��
��С�����뻬�����ļ��ٶȴ�СΪ��a2=$\frac{��Mg}{M}=��g=2m/{s}^{2}$��
�������ȼ���ֱ���˶���ʱ��Ϊ��t1=$\frac{{v}_{1}}{{a}_{1}}=\frac{2}{2}s=1s$��
�������˵���С�����Ϸ���С�������������˶������ʱ��Ϊ��${t}_{2}=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2��0.8}{10}}s$=0.4s��1s��
����С�����ʱ���뻬���ˮƽλ��Ϊ��x=v1t2-$\frac{1}{2}{a}_{2}{t}_{2}^{2}$=$2��0.4m-\frac{1}{2}��2��0��{4}^{2}m=0.64m$��
С�����ʱ����Ҷ˵�ˮƽ����Ϊ��X=x+L=0.64m+2m=2.64m��
�𣺣�1��С�����뻬��֮ǰ������ļ��ٶȴ�С3m/s2��
��2��С�����ʱ����Ҷ˵�ˮƽ����2.64m��
���� ����ţ�ٵڶ����ɵ��ۺ�Ӧ�����⣬�ؼ���Ū���������˶����̺��������������ţ�ٵڶ����ɻ��˶�ѧ�ļ��㹫ʽ�����ٶȣ��ٸ�����ĿҪ����н��֪�����ٶ�����ϵ����ѧ���˶�ѧ��������


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �����������ͷ����ﵽ��β�ٶ�����ʱ��Ϊt�������������λ��Ϊ$\frac{vt}{2}$ | |
| B�� | �����ijһʱ����������ʱ�ļ��ٶ�Ϊa���������ʱ���ٶ�Ϊ$\sqrt{2ah}$ | |
| C�� | �����ijʱ����ļ��ٶ�Ϊa����ʱ�����ܵ��Ŀ�������Ϊmg-ma | |
| D�� | �������������tʱ�䣬ͨ����λ��Ϊy����ù��̵�ƽ���ٶ�һ��Ϊ$\frac{y}{t}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������$\frac{3F}{8}$ | B�� | ������$\frac{F}{8}$ | C�� | 0 | D�� | ������$\frac{F}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ˮƽ��ǿ�糡�У����������������Ĵ���С��M��N�ֱ���ͼʾ·���ƶ���ͬһˮƽ���ϵIJ�ͬλ�ã��ͷź�M��N���־�ֹ��������
��ˮƽ��ǿ�糡�У����������������Ĵ���С��M��N�ֱ���ͼʾ·���ƶ���ͬһˮƽ���ϵIJ�ͬλ�ã��ͷź�M��N���־�ֹ��������| A�� | M�Ĵ�������N�Ĵ� | B�� | M������ɡ�N������� | ||
| C�� | �ƶ���������ǿ�糡��M������ | D�� | �ƶ���������ǿ�糡��N������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
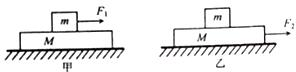 ������ΪM����ľ����ڹ⻬ˮƽ���ϣ���ľ����е��������ȫ��ͬ��������Ϊm����飬��֪M��m���ִӾ�ֹ��ʼ�ֱ�������ľ���ϸ�����ˮƽ����F1��F2����ͼ�ס�����ʾ����֪����ľ��֮��Ķ�Ħ��������ͬ����ľ�峤��Ҳ��ͬ������˵����ȷ���ǣ�������
������ΪM����ľ����ڹ⻬ˮƽ���ϣ���ľ����е��������ȫ��ͬ��������Ϊm����飬��֪M��m���ִӾ�ֹ��ʼ�ֱ�������ľ���ϸ�����ˮƽ����F1��F2����ͼ�ס�����ʾ����֪����ľ��֮��Ķ�Ħ��������ͬ����ľ�峤��Ҳ��ͬ������˵����ȷ���ǣ�������| A�� | ��ͼ�У�����F1�Ĵ�С��Σ�ֻҪF1����ʱ���㹻����������ľ��Ϳɷ��� | |
| B�� | ��ͼ�У�ֻ��F2�Ĵ�С����ijһֵʱ���ſ���ʹ����ľ����� | |
| C�� | ʹ����ľ��������С������F1��F2 | |
| D�� | ʹ����ľ��������С������F1��F2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��ˮƽ�����Ϲ̶�һ�㹻���Ĺ⻬б�棨�����������ƣ�������Ϊm��С���Գ��ٶ�v0��б��˳���б�棬��С����б�������˶��Ĺ����У�������
��ͼ��ʾ��ˮƽ�����Ϲ̶�һ�㹻���Ĺ⻬б�棨�����������ƣ�������Ϊm��С���Գ��ٶ�v0��б��˳���б�棬��С����б�������˶��Ĺ����У�������| A�� | С�����ٶ�v0��б��������ֱ���˶� | |
| B�� | С���ܵ�������б���֧��������б�����ϵij��� | |
| C�� | С���ܵ���֧������СΪmgsin�� | |
| D�� | С���ܵ���֧������СΪmgcos�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ����Ϊ��Բ�ε������ڱڹ⻬������ΪM�����ڹ⻬ˮƽ���ϣ�����һ����Ϊm��С�������ܵ�һ��ˮƽ���ҵ���F���������ȼ����˶�ʱ��С����ͼʾλ�ã���ʱС�����Բ���ѹ����СΪ��������
��ͼ��һ����Ϊ��Բ�ε������ڱڹ⻬������ΪM�����ڹ⻬ˮƽ���ϣ�����һ����Ϊm��С�������ܵ�һ��ˮƽ���ҵ���F���������ȼ����˶�ʱ��С����ͼʾλ�ã���ʱС�����Բ���ѹ����СΪ��������| A�� | m$\sqrt{{g^2}-{{��\frac{F}{M+m}��}^2}}$ | B�� | m$\sqrt{{g^2}+{{��\frac{F}{M+m}��}^2}}$ | C�� | m$\sqrt{{g^2}+{{��\frac{F}{m}��}^2}}$ | D�� | $\sqrt{{{��mg��}^2}+{F^2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
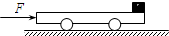 �⻬��ˮƽ���Ͼ���һ�㹻��������M=8kg��С������ͼ��ʾ������С�������ʩ��һ��СF=8N��ˮƽ��������С�������˶����ٶȴﵽv0=1.5m/sʱ����С���Ҷ�����ط���һ����m=2kg��С��飨����Ϊ�ʵ㣩����֪С�����С����Ķ�Ħ��������=0.2��ȡg=10m/s2����
�⻬��ˮƽ���Ͼ���һ�㹻��������M=8kg��С������ͼ��ʾ������С�������ʩ��һ��СF=8N��ˮƽ��������С�������˶����ٶȴﵽv0=1.5m/sʱ����С���Ҷ�����ط���һ����m=2kg��С��飨����Ϊ�ʵ㣩����֪С�����С����Ķ�Ħ��������=0.2��ȡg=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
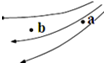
| A�� | �����a���ܵ��糡������ض��볡ǿ����һ�� | |
| B�� | ͬһ���ɷ���a���ܵ��ĵ糡���ȷ���b��ʱ�ܵ��糡���� | |
| C�� | ����ɷ���a�㾲ֹ�ͷţ��ڵ糡���������˶��Ĺ켣��糡��һ�� | |
| D�� | a��ĵ糡ǿ�Ƚϴ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com