
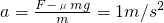
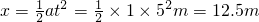
 =
=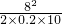 m=16m.
m=16m. 求出滑块在力F作用下经5s通过的位移.
求出滑块在力F作用下经5s通过的位移.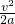 =16m.
=16m. 

科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
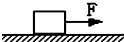 如图所示,一质量为5kg的滑块在F=15N的水平拉力作用下,由静止开始做匀加速直线运动,若滑块与水平地面间的动摩擦因数为0.2(g=10m/s2),求:
如图所示,一质量为5kg的滑块在F=15N的水平拉力作用下,由静止开始做匀加速直线运动,若滑块与水平地面间的动摩擦因数为0.2(g=10m/s2),求:查看答案和解析>>
科目:高中物理 来源: 题型:
 一质量为5kg的滑块在F=15N的水平拉力作用下,由静止开始做匀加速直线运动,若滑块与水平面间的动摩擦因素是0.2,g取10m/s2,问:
一质量为5kg的滑块在F=15N的水平拉力作用下,由静止开始做匀加速直线运动,若滑块与水平面间的动摩擦因素是0.2,g取10m/s2,问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com