
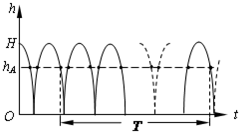
 有一竖直放置、两端封闭的长玻璃管,管内为真空,管内有一小球自某处自由下落(初速度为零),落到玻璃管底部时与底部发生弹性碰撞.以后小球将在玻璃管内不停地上下跳动.现用支架固定一照相机,用以拍摄小球在空间的位置.每隔一相等的确定的时间间隔T拍摄一张照片,照相机的曝光时间极短,可忽略不计.从所拍到的照片发现,每张照片上小球都处于同一位置.求小球开始下落处离玻璃管底部距离(用H表示)的可能值以及与各H值相应的照片中小球位置离玻璃管底部距离的可能值.
有一竖直放置、两端封闭的长玻璃管,管内为真空,管内有一小球自某处自由下落(初速度为零),落到玻璃管底部时与底部发生弹性碰撞.以后小球将在玻璃管内不停地上下跳动.现用支架固定一照相机,用以拍摄小球在空间的位置.每隔一相等的确定的时间间隔T拍摄一张照片,照相机的曝光时间极短,可忽略不计.从所拍到的照片发现,每张照片上小球都处于同一位置.求小球开始下落处离玻璃管底部距离(用H表示)的可能值以及与各H值相应的照片中小球位置离玻璃管底部距离的可能值.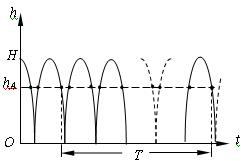
 τ2=
τ2=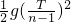 n=2,3,4,…(6)
n=2,3,4,…(6) τ2 n=2,3,4,…(7)
τ2 n=2,3,4,…(7) ]n=3,5,7,???(8)
]n=3,5,7,???(8) τ,由(6)式、(7)式求得Hn的可能值
τ,由(6)式、(7)式求得Hn的可能值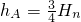 [
[ ]n=2,4,6,????(9)
]n=2,4,6,????(9) τ2=
τ2= n=2,3,4,???(11)
n=2,3,4,???(11)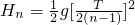 } n=2,3,4,???(12)
} n=2,3,4,???(12)

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中物理 来源:闸北区高三年级物理学科练习卷 题型:038
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com